SOLUCION DE
PROBLEMAS
VIGAS
Prepara tus exámenes
Prepara tus exámenes y mejora tus resultados gracias a la gran cantidad de recursos disponibles en Docsity
Consigue puntos base para descargar
Gana puntos ayudando a otros estudiantes o consíguelos activando un Plan Premium
Orientación Universidad
Prepara tus exámenes
Prepara tus exámenes y mejora tus resultados gracias a la gran cantidad de recursos disponibles en Docsity
Busca documentos
Prepara tus exámenes con los documentos que comparten otros estudiantes como tú en Docsity
Busca documentos en el Store
Los mejores documentos en venta realizados por estudiantes que han terminado sus estudios
Video Cursos
Estudia con lecciones y exámenes resueltos basados en los programas académicos de las mejores universidades
Quiz
Responde a preguntas de exámenes reales y pon a prueba tu preparación
Consigue puntos base para descargar
Gana puntos ayudando a otros estudiantes o consíguelos activando un Plan Premium
Comunidad
Pregúntale a la comunidad
Pide ayuda a la comunidad y resuelve tus dudas de estudio
Ranking de las universidades
Descubre las mejores universidades de tu país según los usuarios de Docsity
Ebooks gratuitos
¡Nuestros e-books salva-estudiantes!
Descarga nuestras guías gratuitas sobre técnicas de estudio, métodos para controlar la ansiedad y consejos para la tesis preparadas por los tutores de Docsity
SOLUCION DE PROBLEMAS DE VIGAS, Ejercicios de Estática
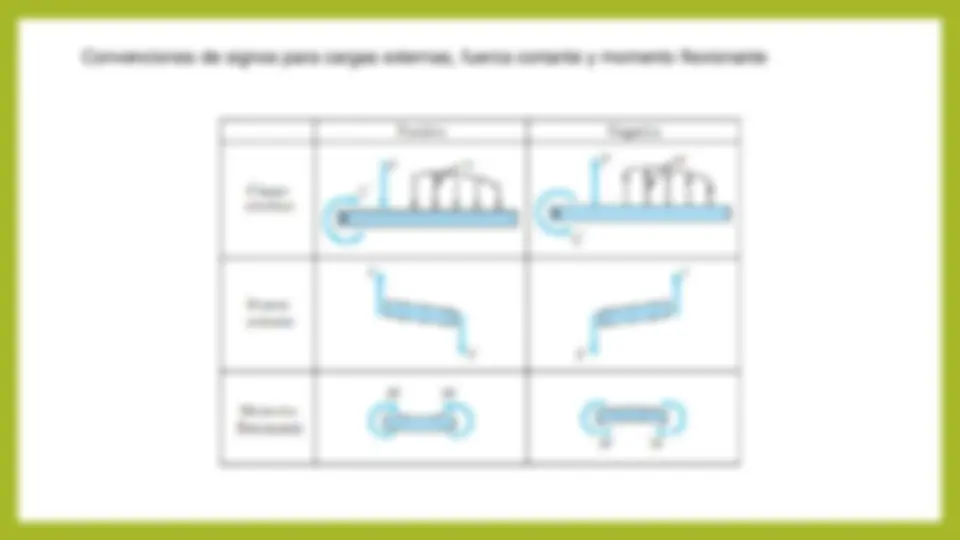
SOLUCION DE PROBLEMAS DE VIGAS
Tipo: Ejercicios
2023/2024
1 / 24
Esta página no es visible en la vista previa
¡No te pierdas las partes importantes!
Documentos relacionados
Vista previa parcial del texto
¡Descarga SOLUCION DE PROBLEMAS DE VIGAS y más Ejercicios en PDF de Estática solo en Docsity!
SOLUCION DE
PROBLEMAS
VIGAS
ANALISIS DE EQUILIBRIO
Problema 1 Determine la fuerza normal interna, la fuerza cortante y el momento flexionante en la viga en los puntos C y D. Suponga que el soporte en B es un rodillo. El punto C está localizado justo a la derecha de la carga de 8 kip.
8 𝑝𝑖𝑒𝑠 = 7 𝑘𝑖𝑝
Fuerzas Internas: Aplicamos ecuaciones de equilibrio en el segment AC ↶ + 𝑀𝑐 = 0
+→ 𝐹𝑥 = 0 𝑁𝑐 =^0
𝑀𝑐 − 7 ( 8 ) = 0 𝑀𝑐 = 56 kip. pie
8 𝑝𝑖𝑒𝑠
Fuerzas Internas: Aplicamos ecuaciones de equilibrio en el segment BD ↶ + 𝑀𝐷 = 0
+→ 𝐹𝑥 = 0 𝑁𝐷 =^0
𝑀𝐷 = 48 kip. pie
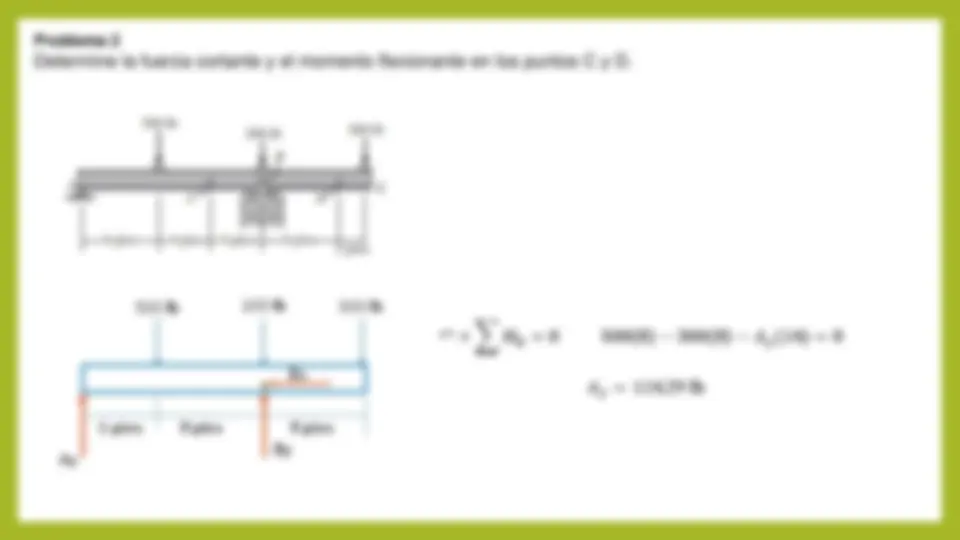
Problema 2 Determine la fuerza cortante y el momento flexionante en los puntos C y D. 500 lb 200 lb^300 lb 6 pies 8 pies 8 pies Ay Bx By
𝐴𝑦 = 114. 29 lb
500 (12) lb 6 pies (^) 6 pies Ay Ax 𝐹𝐵
Momento en el punto A: ↶ + 𝑀𝐴 = 0 𝐹𝐵 cos 30 ° 12 − 500 ( 12 )( 6 ) − 1500 = 0 𝐹𝐵 = 3608. 44 lb 3 pies 𝐹𝐵 = 3608. 44 𝑙𝑏
3 pies 500 (6) lb ↷
→
𝐹𝑋 = 0 −𝑁𝐶^ −^3608.^44 𝑠𝑒𝑛^ 30°^ =^ 𝟎 +↑ 𝐹𝑌 = (^0) 𝑉 𝐶 +^3908.^44 cos^30 °^ −^500 (^6 )^ =^0 ↶ + 𝑀𝑐 = 0
- 44 cos 30 ° 6 − 500 6 3 − 𝑀𝐶 = 0 𝑁𝐶 = − 1804 𝑙𝑏 𝑉𝐶 = − 125 lb 𝑀𝐶 = 9750 𝑙𝑏. 𝑓𝑡 Fuerza normal, momento flexionante y fuerza cortante en el punto C: 𝐸𝑙 𝑠𝑖𝑔𝑛𝑜 𝑛𝑒𝑔𝑎𝑡𝑖𝑣𝑜 𝑒𝑛 𝑁𝐶 𝑦 𝑒𝑛 𝑉𝑐 𝑖𝑛𝑑𝑖𝑐𝑎 𝑞𝑢𝑒 𝑎𝑐𝑡𝑢𝑎 𝑒𝑛 𝑠𝑒𝑛𝑡𝑖𝑑𝑜 𝑜𝑝𝑢𝑒𝑠𝑡𝑜 𝑎𝑙 𝑞𝑢𝑒 𝑠𝑒 𝑚𝑢𝑒𝑠𝑡𝑟𝑎 𝑒𝑛 𝑒𝑙 𝐷𝑖𝑎𝑔𝑟𝑎𝑚𝑎 𝑑𝑒 𝑐𝑢𝑒𝑟𝑝𝑜 𝑙𝑖𝑏𝑟𝑒
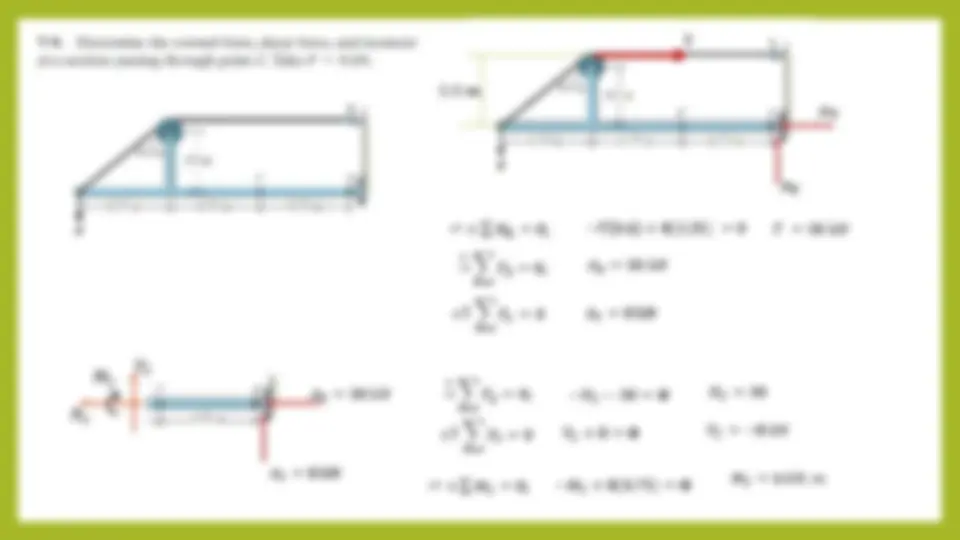
0.6 m
T
Ay Ax ↶ + σ^ 𝑀𝐴 = 0 ; −𝑇^0.^6 +^8 (^2.^25 )^ =^0 𝑇 = 30 𝑘𝑁 →
𝐹𝑋 = 0 ; 𝐴𝑋 =^30 𝑘𝑁 +↑ 𝐹𝑌 = 0 𝑉𝐶 𝑁𝐶
↷ 𝐴𝑋 = 30 𝑘𝑁 𝐴𝑌 = 8 kN 𝐴𝑌 = 8 kN →
𝐹𝑋 = 0 ; (^) −𝑁𝐶 − 30 = 𝟎 𝑁𝐶 =^30 +↑ 𝐹𝑌 = 0 𝑉𝐶 +^8 =^ 𝟎^ 𝑉𝐶^ =^ −^8 𝑘𝑁 ↶ + σ^ 𝑀𝐶 = 0 ; −𝑀𝐶 +^8 (^0.^75 )^ =^ 𝟎^ 𝑀𝐶 = 6 𝑘𝑁. 𝑚
6 cos 45° 2 (6)=12 kN Ay Ax By ↶ + σ 𝑀𝐴 = 0 ; 𝐵𝑦(^6 +^6 cos^45 °)^ −^12 (^3 +^6 cos^ 45°)^ =^0 𝐵𝑦^ =^8.^485 kN →
𝐹𝑋 = 0 ; +↑ 𝐹𝑌 = 0 𝐴𝑦^ +^8.^485 −^12 =^0 𝐴𝑦 = 3. 515 kN 𝐴𝑥 = 0
↶ + σ^ 𝑀𝐴 = 0 ; 𝐵𝑦 4 −^1000 2 =^0 𝐵𝑦^ =^500 N 1 2
0.5 m 1.5 m
↶ + σ^ 𝑀𝑐 = 0 ; − 500 4 + 225 0. 5 + 𝐵𝑥 1. 5 = 0 𝐵𝑥 = 1258. 33 N
0.5 m 1.5 m
𝐵𝑥 = 1258. 33 N
𝐵𝑦 = 500 N
↷
→
𝐹𝑋 = 0 ; +↑ 𝐹𝑌 = 0 ↶ + σ 𝑀𝐸 = 0 ;
−𝑁𝐸 − 1258. 33 − 225 = 0 𝑁𝐸 =^1.^48 𝑘𝑁
𝑉𝐸 − 500 = 0 𝑉𝐸 = 500 N
−𝑀𝐸 + 225 0. 5 + 1258. 33 1. 5 − 500 ( 2 ) = 0 𝑀𝐸 =^1000 N.m
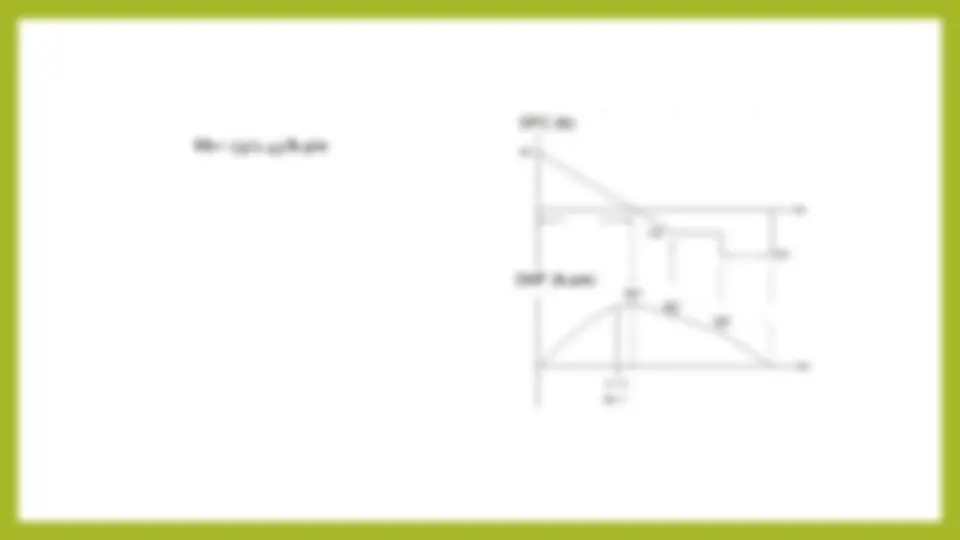
Mx= 1371.43 lb.pie
a) Elaborar los diagramas de fuerza cortante y de momento flector con los valores de la fuerza cortante y del momento flector, indicados a l0 largo de toda la viga. b) Determinar las ecuaciones de la fuerza cortante y del momento flector en cada tramo de la viga.