

















Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
An overview of matalas (1967) multisite normal generation model for multivariate stochastic processes. The model preserves the mean, variance, lag one serial correlation, lag one cross-correlation, and lag zero cross-correlation. The equations for generating the first two values of data from two sites and calculating the cross-correlation matrices of lag zero and lag one.
Typology: Study notes
1 / 24

This page cannot be seen from the preview
Don't miss anything!
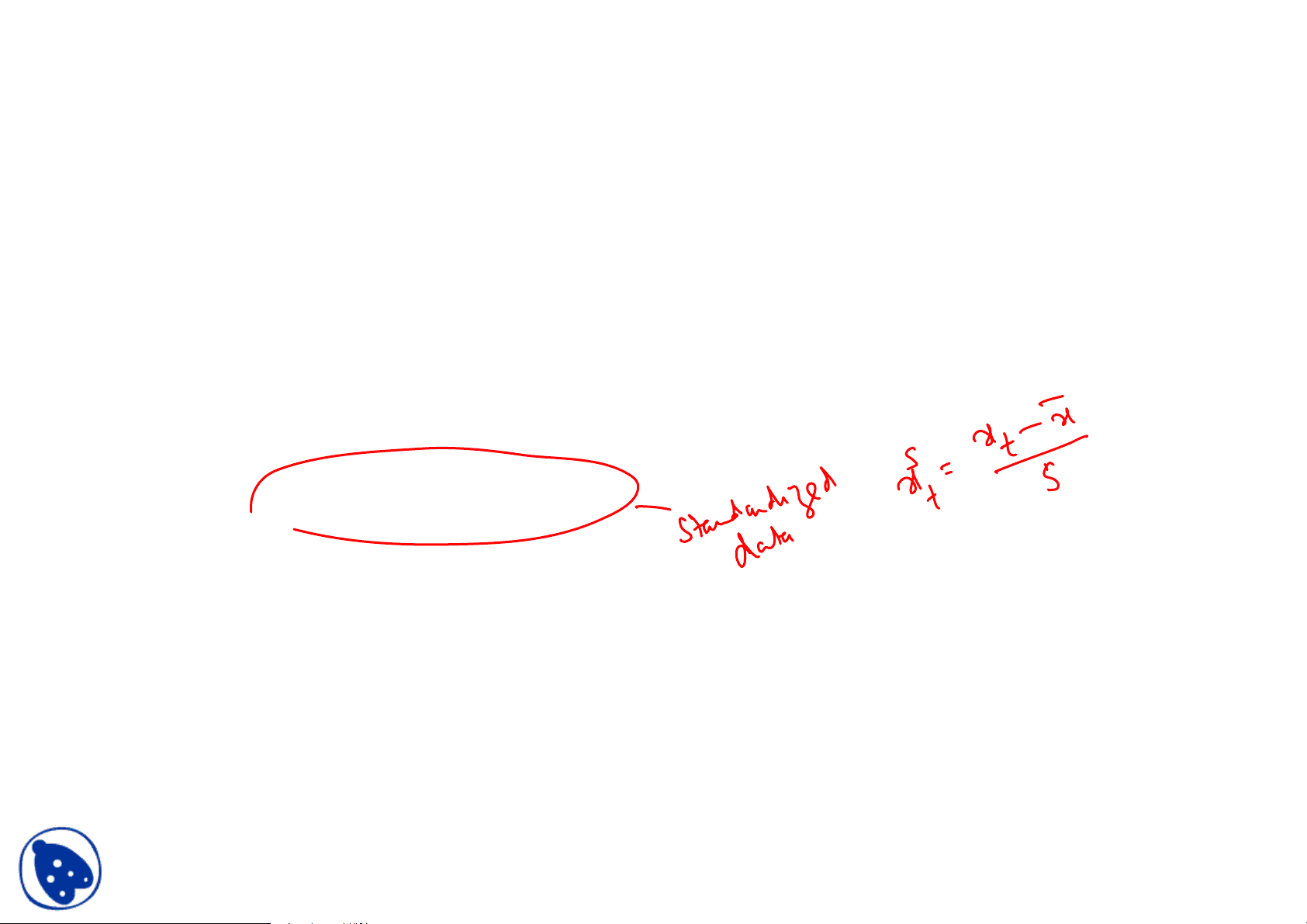
















t
t+
Multivariate Stochastic models
3
t 1 t t 1
X AX B ε
= +
Ref.: Matalas, N.C. (1967) Mathematical assessment of synthetic hydrology, Water
Resources Research 3(4):937-
ε
t+
is N(0,1); p x 1 vector with ε
t+
t
Multivariate Stochastic models
4
0 t t
M E X X ⎡ ⎤ =
⎣ ⎦
( )
, ,
0
1
n
j t j i t i
t i j
=
∑
0
Multivariate Stochastic models
6
( )
, 1 ,
1
2
n
j t j i t i
t i j
−
=
∑
Q is the original random variable before
standardization e.g., stream flow
t
Multivariate Stochastic models
7
t 1 t t 1
X AX B ε
= +
t 1 t t t t 1 t
E X X AE X X BE ε X
⎡ ⎤ ⎡ ⎤ ⎡ ⎤ = +
⎣ ⎦ ⎣ ⎦ ⎣ ⎦
M AM 0
A M M
= +
=
ε
t+
t
9
1 t t 1
t t
t t
t t
1 t t 1
Multivariate Stochastic models
10
{ }
t t t t t
t t t t
X AX B
X A B
ε ε ε
ε ε ε
= +
= +
0
t t t t t t
t t t t
E X E X A B
E X A E B
IB
B
ε ε ε ε
ε ε ε
⎡ ⎤ ⎡ ⎤ = +
⎣ ⎦ ⎣ ⎦
⎡ ⎤ ⎡ ⎤ = +
⎣ ⎦ ⎣ ⎦
= +
=
t+
Multivariate Stochastic models
12
( )
( ) ( )
( ) ( ) ( )
( ) ( ) ( )
( ) ( )
( )
'
b b b b p
b b b b p
b p b p b p p b p p
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
( ) ( ) ( )
c c c c p
c c c c p
c p c p c p p
Multivariate Stochastic models
13
( ) ( )
( ) ( ) ( ) { }
1,1 1,
2, 2 2, 2 2,
b c
b c b
=
= −
( ) ( ) ( ) ( ) ( ) { }
1
2 2 2 2
th
15
Example – 1
16
Example – 1 (Contd.)
( ) ( )
( ) ( )
0 0
0 0
r r
M
r r
⎡ ⎤
=
⎢ ⎥
⎣ ⎦
18
Example – 1 (Contd.)
( )
( ) ( )
( )
, , 1
1
,
1
1
n
P i P Q i Q
i
P Q
P Q
x x x x
r
n s s
=
− −
=
−
∑
0.302 0.
0.02 0.
M
⎡ ⎤
=
⎢ ⎥
−
⎣ ⎦
A M M
=
2.73 2.
2.17 2.
M
− ⎡ ⎤
=
⎢ ⎥
−
⎣ ⎦
19
Example – 1 (Contd.)
A M M
=
0.302 0.164 2.73 2.
0.02 0.118 2.17 2.
− ⎡ ⎤ ⎡ ⎤
=
⎢ ⎥ ⎢ ⎥
− −
⎣ ⎦ ⎣ ⎦
0.47 0.
0.31 0.
A
− ⎡ ⎤
=
⎢ ⎥
−
⎣ ⎦
21
Example – 1 (Contd.)
( ) ( ) ( )
b 1,1 = c 1,1 = 0.89 = 0.
( ) ( ) ( )
( )
1,1 0.89, 1, 2 2,1 0.76,
2, 2 0.
c c c
c
= = =
=
( )
( )
( )
2,
2,1 0.
1,1 0.
c
b
b
= = =
( ) ( ) ( ) { }
{ }
2, 2 2, 2 2,
0.95 0.81 0.
b = c − b
= − =
( )
( )
( )
,
,
1,
c k
b k
b
=
22
Example – 1 (Contd.)
( ) ( ) ( )
b 1,1 = 0.94, b 2,1 = 0.81, b 2, 2 =0.
0.94 0
0.81 0.
B
⎡ ⎤
=
⎢ ⎥
⎣ ⎦
t 1 t t 1
X AX B ε
= +
0.47 0.21 0.94 0
0.31 0.37 0.81 0.
P t P t P t
Q t Q t Q t
x x
x x
ε
ε
⎡ ⎤ − ⎡ ⎤ ⎡ ⎤ ⎡ ⎤ ⎡ ⎤
= +
⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥
−
⎣ ⎦ ⎣ ⎦ ⎣ ⎦ ⎣ ⎦ ⎣ ⎦