
























Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
Introduction to probability and statistics
Typology: Exercises
1 / 39

This page cannot be seen from the preview
Don't miss anything!
































dr hab.in
ż. Katarzyna Zakrzewska, prof.AGHKatedra Elektroniki, AGHe-mail: zak@agh.edu.plhttp://home.agh.edu.pl/~zak
1
http://physics.nist./gov/UncertaintyWyra
żanie Niepewno
ści Pomiaru. Przewodnik. Warszawa, G
łówny Urz
ąd Miar 1999
In October 1992, a new policy on expressing measurement uncertaintywas instituted at NIST, National Institute of Standards and Technology.Elaboration of
Guide to Expression of Uncertainty in Measurement
by
International Organization for Standardization,
ISO, 1993
2
Applicable to results associated with: •^ international comparisons of measurement standards, •^ basic research, •^ applied research and engineering, •^ calibrating client measurement standards, •^ certifying standard reference materials, and •^ generating standard reference data.
In the course of measurements values different fromthose predicted by theory are obtained. The source ofdiscrepancies between theory and experiment can betraced back to imperfections due to:-experimentalist,-measuring equipment,-object measuredMore
perfect
the
experiment
is^
made,
discrepancies
decrease. Error, uncertainty
can be reduced.
4
Result of a measurement should be given in one ofthe following forms:
2
Example: In an experiment, the electrochemical equivalentk was found to be:
k=0,
g/C
∆k=0,
g/C How one can express this result?
significant digits
Non-significant digits
Answer. k= (0,
±^ 0,00004) g/C
or
k= 0,00110(4) g/C
5
Quantities given by formulas (1) and (2) are singularrealization
of
random
variable
which
is
why
they
cannot
be
treated
by
theory
of
uncertainty.
Practically, we do not know real values and estimate uncertainties,
due to dispersion of results, from the
laws of
statistics
Uncertainty
is
-^ a
parameter
related
to^
the
result
of
measurements, • characterized by
dispersion
-^ assigned to the measurand in a
justified way
7
Absolute uncertainty u
is expressed in the same units as a measurand
Symbols: u or u(x) or u(concentration of NaCl)
Relative uncertainty u
(x)r
the ratio of absolute
uncertainty to the measured value:
xu x x u^ r
)( )( =
Relative uncertainty has no units and can be expressed in %Introduction to probability and statistics. lecture 1
8
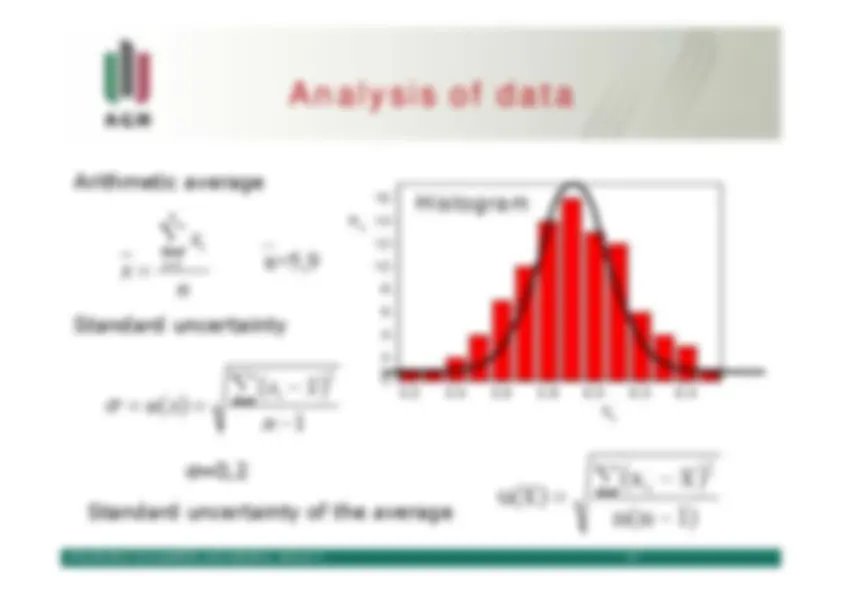
Standard uncertainty
Generally accepted and suggested.
, with ai
dispersion around the average x is characterizedby^
standard deviation
defined as:
Standard uncertainty
represents an estimate of
standard deviation.
(^
) xx n 2 i
limn
∑
=σ
∞→
10
Maximum uncertainty
Within this interval Deterministic measure.
: x^ -^0
∆x
< x
< xi^
∆x
all the results x
, will fall.i^
It is recommended to replace the maximum uncertaintyby a standard uncertainty:
11
x
x^
x^
x0=x^
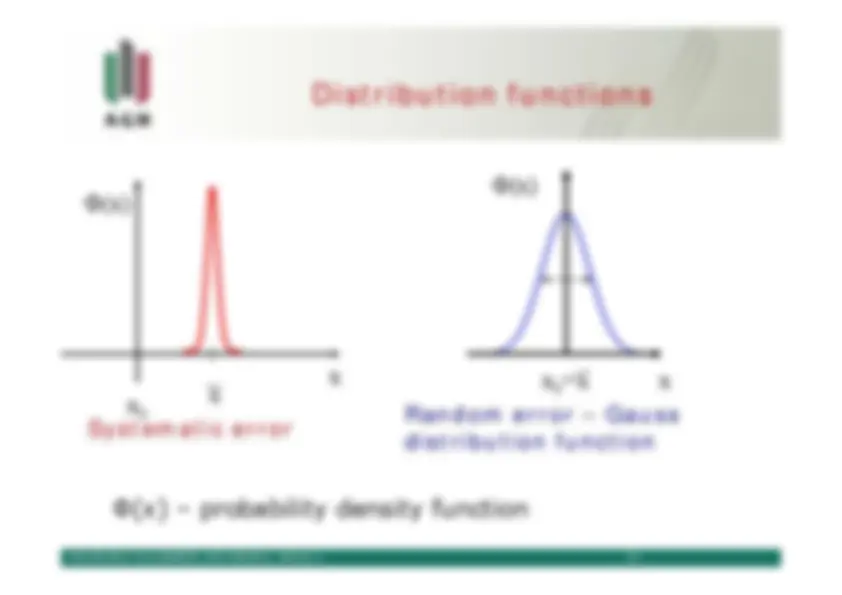
Φ(x)
Φ(x)
Systematic error
Random error – Gaussdistribution function
13
Φ(x) – probability density function
TYPE A
15
Example: We have performed a seriesof measurements getting thefollowing results x
,x 12
, ….x
n.
In such a sample that can beconsidered as big some ofthe results are the same; n
k
is a number of randomexperiments, in which thesame result x
has occurred.k
n^ /n is a frequency of thek result
x^ k^
nk^
n/nk
5,^
1
0,
5,^
1
0,
5,^
2
0,
5,^
4
0,
5,^
7
0,
5,^
10
0,
5,^
14
0,
5,^
16
0,
6,^
13
0,
6,^
12
0,
6,^
6
0,
6,^
4
0,
6,^
3
0,
6,^
1
0,
Sum
94
16
Gauss distribution function
Probability density function for the result x or its error
according to Gauss x^0
is the most probable result and can be represented by the arithmetic average,
σ^ is standard deviation,
(^2) σ is
variance
⎞ ⎟ ⎟ ⎠
⎛^ ⎜⎜ ⎝
− −
= Φ^
(^202) 2
) ( exp 1 2 )(
σ
π σ
x x
x
18
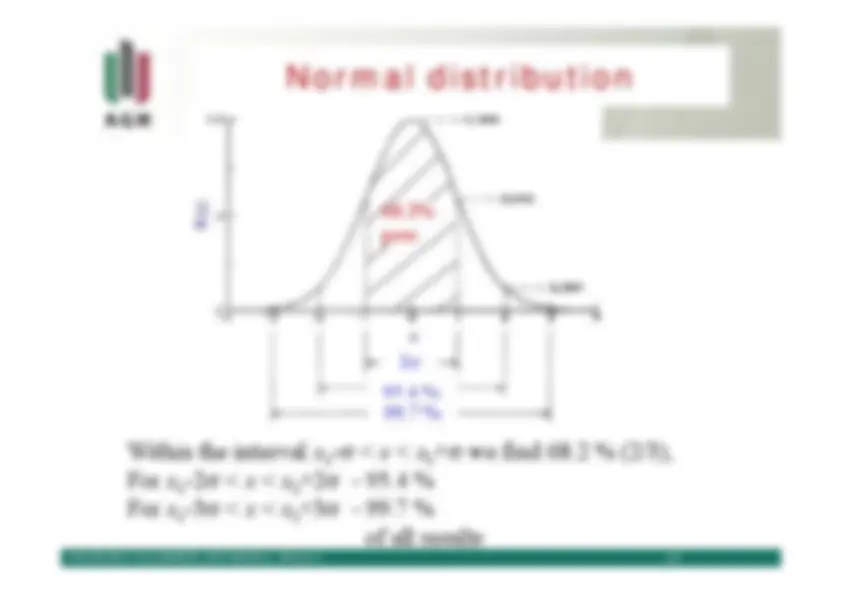
Normal distribution
x 2 σ 95.4 %99.7 %
(x) Φ Within the interval
x - σ^0
<^ x
<^ x
+σ 0 we find 68.2 % (2/3),
For^
x -2^0
σ^ <^
x^ <^
x +2^0
σ^ - 95.4 %
For^
x -3^0
σ^ <^
x^ <^
x +3^0
σ^ - 99.7 %
68.2%pow. of all results
19