
















Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
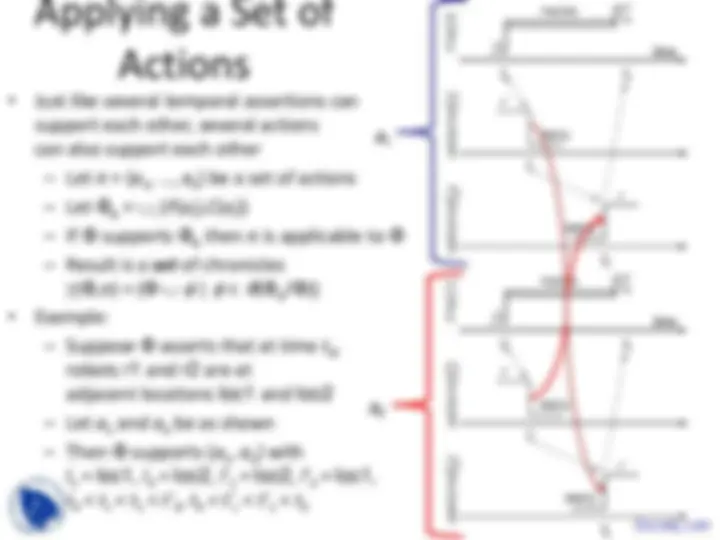
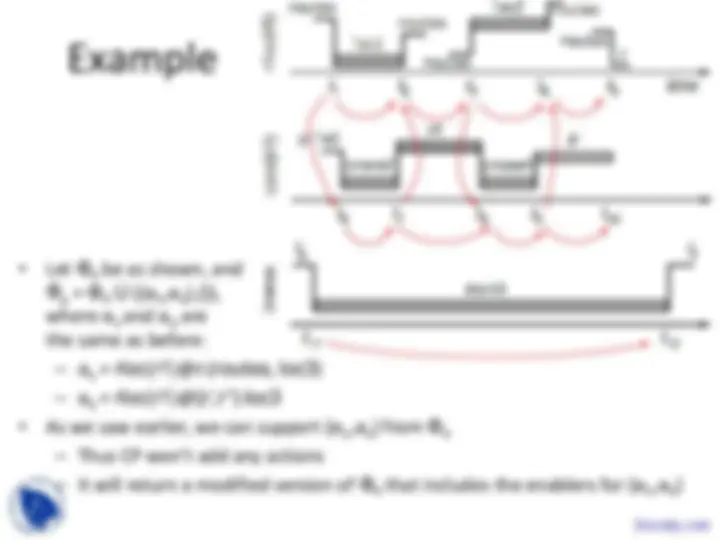
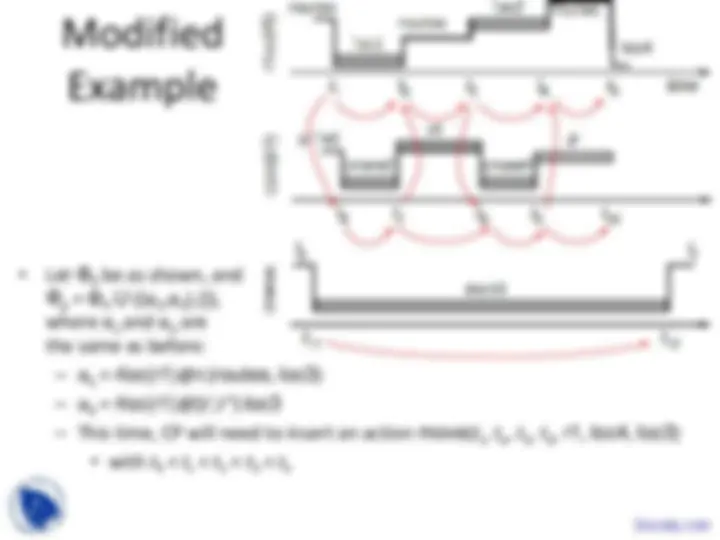
These are the lecture Slides of Automated Planning which includes Domain-Independent Planners, Abstract Search Procedure, Planning Algorithms, Current Set of Solutions, Unpromising Members, Loop Detection, Constraint Violation etc. Key important points are: Temporal Planning, Explicit Representation, Sequence of Discrete Events, State Variables, Persistence Constraints, Time-Oriented View, Partially Specified Function, Temporal Assertions
Typology: Slides
1 / 26

This page cannot be seen from the preview
Don't miss anything!



















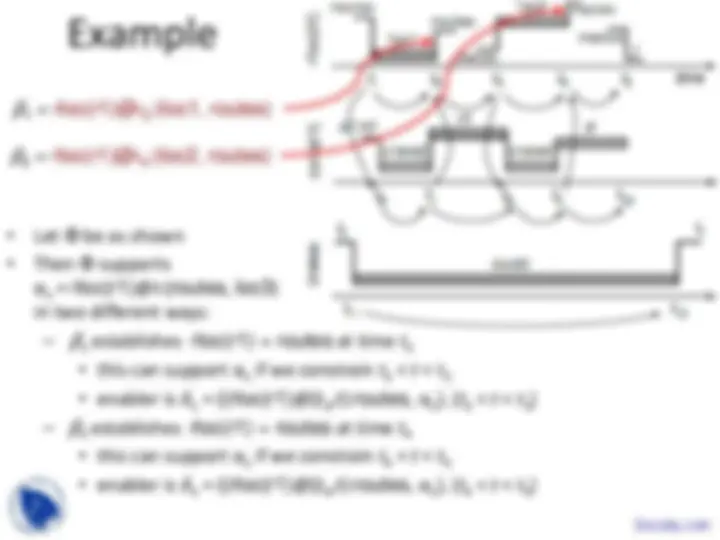
Inconsistency in the book between Figure 14. and Example 14.
C-consistency
move( t (^) s , t (^) e , t 1 , t 2 , r , l , l' ) =
a 1
a 2