






































Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
The polytope algorithm for multivariate unconstrained optimization, a method for finding the minimum of a function when derivatives are not available. The algorithm is detailed step by step with examples in both matlab and hand calculations.
Typology: Study notes
1 / 48

This page cannot be seen from the preview
Don't miss anything!









































Number of functionevaluationsnincreases as e^ , where n is numberof dimensions.
The Polytope Algorithm • This is a direct search method. • Also known as “simplex” method. • In n dimensional case, at each stage wehave n+1 points
Polytope Example • For n = 2 we have three points at eachstep.^ x^1 x 3
a(c - x ) cc - x^33 x^2 (worst point)
x r
Detailed Polytope Algorithm 1. Evaluate F(
MATLAB Example Polytope >> banana = @(x)10*(x(2)-x(1)^2)^2+(1-x(1))^2; >> [x,fval] = fminsearch(banana,[-1.2, 1],optimset('Display','iter'))
Polytope Example by Hand^ (^
)^ (^
) (^
(^2222222) ) (^22)
(^5). (^0) ) (^1) () 2 ( 3
(^5). (^0) ) (^1) ( (^25). 0 ),(
+−−++− −−+− +=^ yx
yx yxyxF
Polytope Example: Step 1 • Polytope is i 1
2 3 x (0,0)i^
(0,0.5)
(0.433,0.25) F( x )^ 9.7918i
7.^
-^ Worst point is
x ,^ c^ = ( x +^ x )/2 = (0.2165,0.375)^123
-^ Relabel points:
x fl^ x ,^ x fl^ x^3113
-^ x =^ c^ +^ a( c -^ x r^
) = (0.433,0.75) and F( 3
x )=3.6774r^
-^ F( x )< F( x ) sor^1
x is best point so try to expand.r^
-^ x =^ c^ +^ b( x - c e^ r^
) = (0.5413,0.9375) and F(
x )=3.1086e
-^ F( x )< F( x ) so accept expander^
After Step 1 2 1 1
2
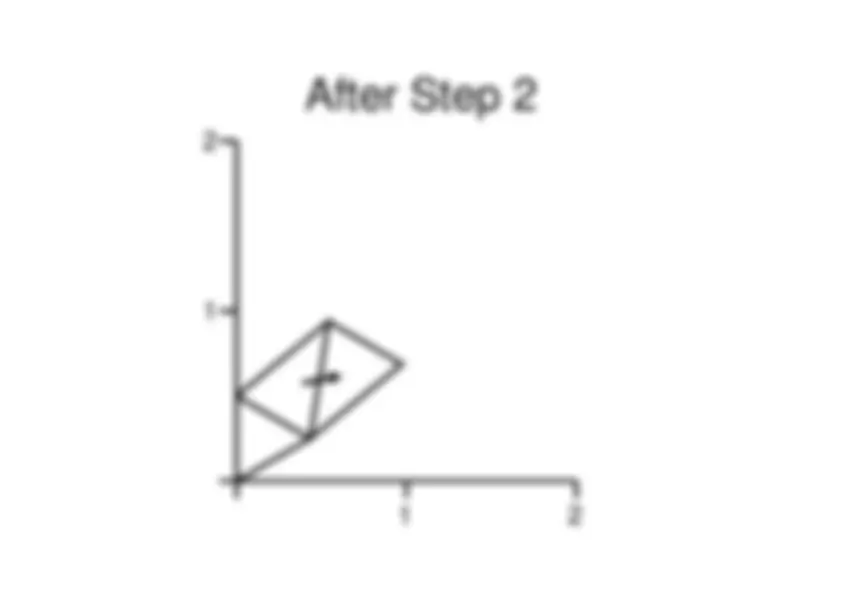
After Step 2 2 1 1
Polytope Example: Step 3 • Polytope is i 1
2 3 x (0.5413,0.9375)i^
(0.433.0.25)^
(0.9743,0.6875) F( x )^ 3.1086i
-^ Worst point is
x ,^ c^ = ( x +^ x )/2 = (0.7578,0.8125)^213
-^ Relabel points:
x fl^ x ,^ x fl^ x ,^3123
x fl^ x^12
-^ x =^ c^ +^ a( c -^ x r^
) = (1.0826,1.375) and F( 3
x )=3.1199r^
-^ F( x )>F( x ) so polytope is too big. Need to contract.r^2 •^ x =^ c^ +^ g( x - c c^ r^
) = (0.9202,1.0938) and F(
x )=2.2476c^
-^ F( x )<F( x ) so accept contraction.c^ r^
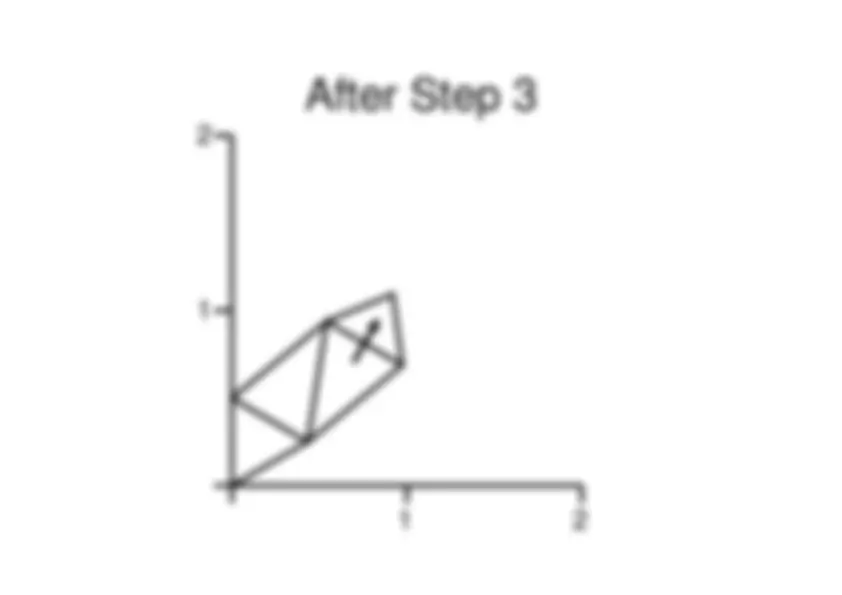
Polytope Example: Step 4 • Polytope is i 1
2 3 x (0.9743,0.6875)i^
(0.5413,0.9375)
(0.9202,1.0938) F( x )^ 2.0093i
-^ Worst point is
x ,^ c^ = ( x +^ x )/2 = (0.9472,0.8906)^213
-^ Relabel points:
x fl^ x ,^ x fl^ x^3223
-^ x =^ c^ +^ a( c - x r^
) = (1.3532,0.8438) and F( 3
x )=2.7671r^
-^ F( x )>F( x ) so polytope is too big. Need to contract.r^2 •^ x =^ c^ +^ g( x - c c^ r^
) = (1.1502,0.8672) and F(
x )=2.1391c^
-^ F( x )<F( x ) so accept contraction.c^ r^
After Step 4 2 1 1
2
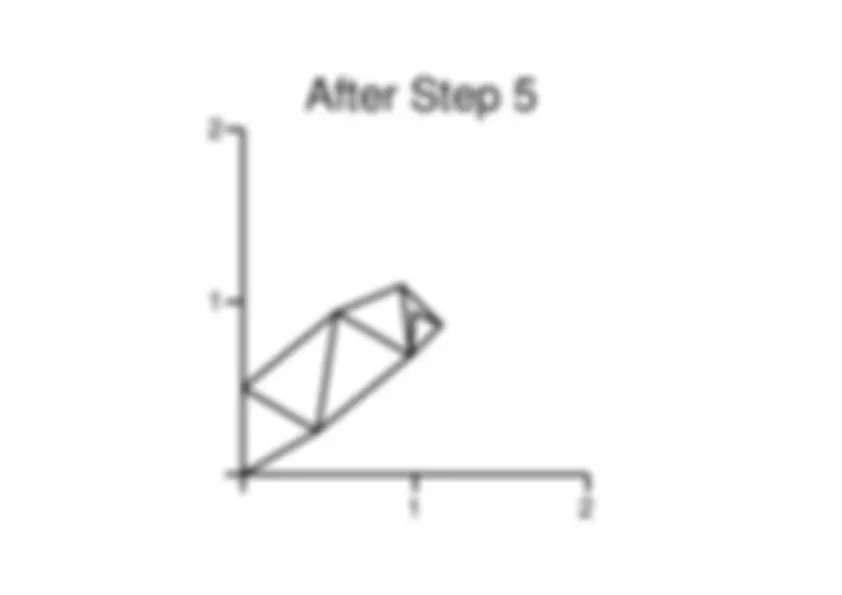
After Step 5 2 1 1
2
Polytope Example: Step 6 • Polytope is i 1
2 3 x (0.9743,0.6875)i^
(1.1502,0.8672)
(0.9912,0.9355) F( x )^ 2.0093i
-^ Worst point is
x ,^ c^ = ( x +^ x )/2 = (0.9827,0.8117)^213
-^ Relabel points:
x fl^ x ,^ x fl^ x^3223
-^ x =^ c^ +^ a( c -^ x r^
) = (0.8153,0.7559) and F( 3
x )=2.1314r^
-^ F( x )>F( x ) so polytope is too big. Need to contract.r^2 •^ x =^ c^ +^ g( x - c c^ r^
) = (0.8990,0.7837) and F(
x )=2.0012c^
-^ F( x )<F( x ) so accept contraction.c^ r^