Propagation of Elastic Waves in a Floating Ice Sheet, Study notes of Microwave Engineering and Acoustics

Download Propagation of Elastic Waves in a Floating Ice Sheet and more Study notes Microwave Engineering and Acoustics in PDF only on Docsity!

Columbia ®nfoersttp

PALISADES. NEW YORK

Lamont Geological Observatory

/ * x / Hi,yv

Technical Report on Seismology

No. 8

Propagation of Elastic Waves in a Floating Ice Sheet

ABSTRACT

The characteristic equation for the propagation of elastic waves in a floating ice sheet is derived and discussed, with special emphasis on the evaluation of phase velocity for very large and very small wavelengths. The solutions cannot be reduced to symmetric and anti-symmetric modes as in the case of a plate in a vacuum or a liquid. Among the waves discussed are com- pressional waves, shear waves, longitudinal waves, flexural waves, Rayleigh waves, Stoneley waves, and Love waves. INTRODUCTION This paper was undertaken as a result of current inter¬ est in the utilization of elastic waves transmitted through a floating ice sheet for determining the thickness and mechanical strength of the ice, for position fixing and long range signalling. The ice sheet is treated as a two dimensional wave guide and the characteristic equation giving the functional dependence between phase velocity and period is derived. From an examination of this equation one can identify the possible waves and determine whether or not they are attenuated. In the derivations which follow the atmosphere is replaced by a vacuum. Air coupling of flexural waves in floating ice has been treated in other papers by Press, Crary, Oliver, and Katz (1950) and by Press and Ewing (1950). INFINITE PLATE IN A VACUUM AND LIQUID The analogous problems of wave propagation in an infinite elastic plate were solved by Lamb (1917) for a plate in a vacuum and by Osborne and Hart (1945) for a plate in a liquid having in¬ finite extent and considerably smaller sound velocity than that for compressional or shear waves in the plate. These writers did not

include SH waves (shear waves polarized horizontally) in their solutions, but fully discussed all other elastic wave types. In the solutions of Lamb, and Osborne and Hart the period equations take the form of fourth and sixth order determinants respectively. These reduce respectively to two second and third order determinants representing motions of the plate which are symmetrical and antisymmetrical about the median plane. For wavelengths small compared to the thickness of the plate the sym¬ metric and antisymmetric solutions reduce to Rayleigh waves trans¬ mitted along the surfaces. These surface waves are attenuated for the case of a plate in a liquid because of losses by acoustic radiation. For short wavelengths there is also a Stoneley type wave travelling along the plate-liquid interfaces with a velocity close to but less than the velocity of sound in the liquid. For wavelengths large compared to the thickness of the plate the antisymmetric solution reduces to flexural waves and the symmetric solution becomes longitudinal waves of an elastic plate. The effect of the liquid on the propagation of the longitudinal waves is to add a small attenuation which increases as the fre¬ quency, The flexural waves, travelling with a velocity less than the speed of sound in the liquid, remain unattenuated in the pres¬ ence of the liquid, although the dispersion is somewhat changed. For long wavelengths the presence of the liquid introduces an ad¬ ditional solution for the symmetric case in which the waves are propagated without attenuation with a velocity very close to that of sound in the liquid. For intermediate wavelengths solutions exist for the plate in a liquid which are closely related to the corresponding

U, = d V?/^X-+ JV./Jz. W] = d^fjdz - J'/'./o'x

aA= diPa./J* (^2 )

where u and w are the horizontal and vertical particle displace¬ ments. SH waves are not included in this discussion and will be treated more simply in a later section. The vertical stress pzz and the tangential stress p^ can be expressed in terms of Cf} {jj and the elastic constants as follows: Hz-A 4 A//( Cflp/fr'- - d'P/J*dz)

■fax - //(d^/dz- - d^tp/dX2- + 5. d2(f/dxdz)

(3)

It is required that the functions and Vj/ satisfy the wave equations

in the ice

in the ice (^) ( 4 )

in the liquid and the boundary conditions

(PZZ>1 : 0

(Pjx)l = 0

at z = -H at z i -H (Pzz)l • ^zz^

(Pzx)l = 0

at z : H (^) ( 5 ) at z = H W1 = w2 at^ z^ :^ H

It can readily be verified that solutions of (4) are of the form: -b £3 CoH'ty ($zj~\ X-ul^)J

V, - [C \L (><-<> t)J ( 6 )

where ?= k' (/ - cxMr)

l= *Y/- cY/3/1) j’Y * (l-zx/vc)

and c = uJ/k. In equation (6) , and make up a system of waves progressing in the x direction with a phase velocity c and wavelength L related to the wave number k by k - 27//L. The frequency f is given by f z U)/27/ = ck/277. is taken to decrease exponentially with depth in the liquid since we are particularly interested in the case where no energy is lost by refraction into the liquid. If equations (6) are substituted in the boundary condi¬ tions (5), using (2) and (3), five independent homogeneous equa¬ tions in the unknown amplitude coefficients A, B, C, D, E, are obtained. Any four of the unknowns can be found in terms of the fifth. For a solution of all five to exist, however, the fifth order determinant of their coefficients must vanish. The charac¬ teristic equation is the condition for the determinant to vanish.

Poisson's assumption is made at this point to simplify our equations. Thus we take Poisson's constant <T : 0.25 for ice, so that X, - M< • Although observed values of/for lake ice run

The period equation (8) defines an implicit relation between the phase velocity c and the wave number k. The dependence of c on cd can be obtained by substituting k = &)/c in (8). Real values of c and k which satisfy (8) correspond to propagation without attenuation* Complex values of c or k for real u) cor¬ respond to propagation with attenuation, the degree of attenuation increasing with the magnitude of the imaginary component* The energy loss associated with damped propagation is due to radiation from the ice sheet into the liquid* From equation (8) it is seen that c z o<, and c Z /3f are solutions which satisfy the characteristic equation for all frequencies•

EVALUATION OF PHASE VELOCITY FOR VERY SMALL WAVELENGTHS For wavelengths small compared to the thickness of the ice sheet (kH large) P = Q and equation (8) reduces to

and

(yf+ >+$TpK^ + ^ = 0 (ii)

Equation (10) is the same expression derived by Lamb for a plate in a vacuum and corresponds to Rayleigh waves propagated along the free surface of a semi-infinite solid medium. The algebraic solution of (10) for c gives the well known result for Rayleigh waves cR - *9194/?, • Equation (11) is identical to the expression derived by Osborne and Hart for a plate in a liquid and corresponds to Rayleigh waves propagated along the interface between a semi-

infinite liquid and solid medium. Following Osborne and Hart the phase velocity can be deduced approximately from (11) by substi¬

tuting c r c^ (1 + £ ), (6 <l)in (11). If f is small we may

write approximately

Using f? = .917 /£,/?,= 6300 ft/sec, v2 = 4800 ft/sec,

~)3/9i > we obtain approximately £ z .25 i.

The reduction of the period equation (8) into the al¬ gebraic expressions (10) and (11) for wavelengths small compared to the plate thickness is simply interpreted. For these wave¬ lengths the ice sheet is effectively infinitely thick and the propagation reduces to Rayleigh waves propagated without attenua¬ tion at the free surface and attenuated Rayleigh waves trans¬ mitted along the bottom surface, continuously radiating energy to the liquid. Equation (11) can also be satisfied by c real and less than v 2. This can be seen by rewriting (11) in the following form;

The first and seco nd terms of (13) are of opposite sign, so that

If (17) is compared with the solution C//Z, - &( ^ for

a plate in a vacuum it is seen that the presence of the liquid hardly affects the real part of the phase velocity, but adds a small attenuation, which for large wavelengths increases as the inverse cube of wavelength. This is in agreement with the experi¬ mental work of Ewing, Crary, and Thorne (1934) whose determination of the velocity of longitudinal waves in floating lake ice checks the velocity given by the real part of (17). For long wavelengths (16) gives for the velocity of flexural waves:

/*/^ &-<- /^ (i.)

In obtaining (18) third order terms must be included in the ex¬ pansion of the hyperbolic functions. For a plate in a vacuum the

corresponding solution is cfa?= (V/3)f H) (l-/%, fa?) , it is

interesting to note that (18) can be reduced to the corresponding expression for a plate in a liquid simply by replacing by 2 fa • The steady state plane wave theory of long flexural waves in an ice sheet on water of either finite or infinite depth was given by Ewing and Crary (1934). The results for the latter case were extended by Press and Ewing (1951) for waves originating in an impulsive point source. The observed dispersion and ampli¬ tude of explosion generated flexural waves on lake ice are shown to be in reasonable agreement with theory in these papers. At cer¬ tain frequencies flexural waves in ice are strongly coupled to the atmosphere. This phenomenon has been discussed by Press, Crary, Oliver, and Katz (1951) and Press and Ewing (1951).

EVALUATION OF PHASE VELOCITY FOR INTERMEDIATE WAVELENGTHS

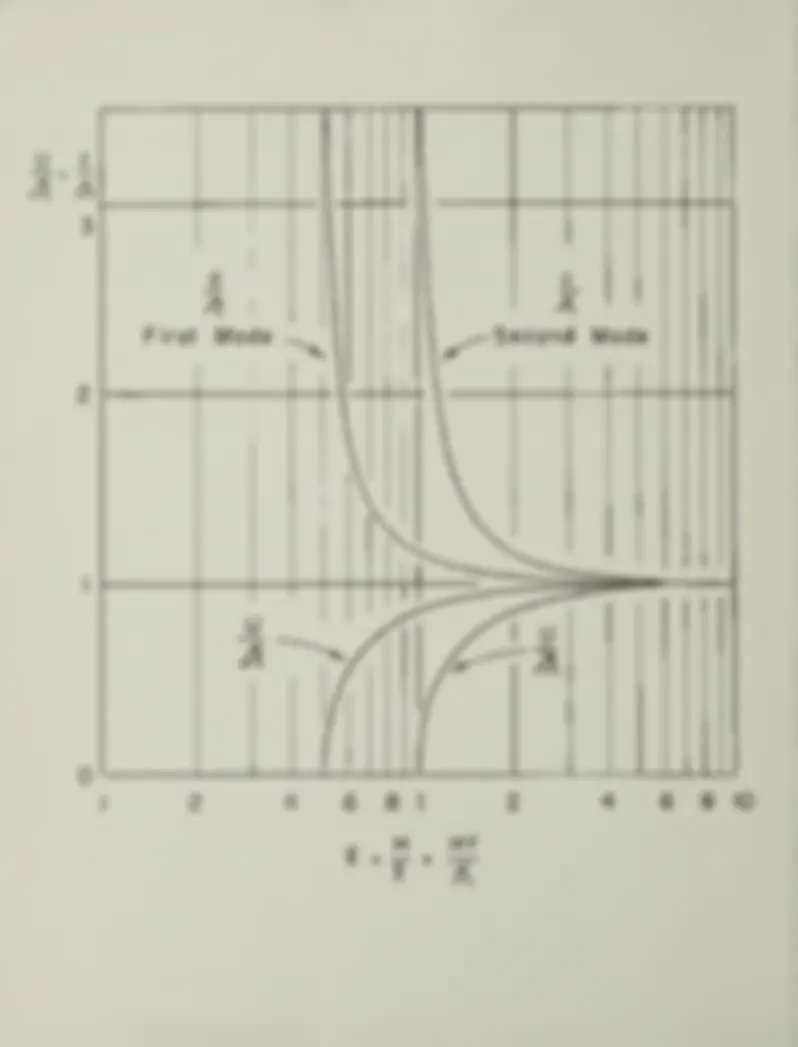
Unlike the results for a plate in a vacuum or a liquid, the characteristic equation does not reduce to symmetric and anti¬ symmetric modes* We are left with a complicated expression (equation (8)) which makes the evaluation of phase velocity as a function of wavelength or frequency an exceedingly difficult task for intermediate wavelengths. Such calculations would indicate how the high and low frequency values of phase velocity discussed above connect up. In general for c > v„ the phase velocity has an imaginary component, indicating attenuation due to radiation from the sheet into water. Both real and imaginary components of phase velocity are frequency dependent, the waves being dispersive as well as selectively attenuated. For c < v, no energy losses due to radiation into the water occur and the waves are propa¬ gated as a dispersive, unattenuated train. LOVE WAVES IN A FLOATING ICE SHEET The theory of Love waves in a floating ice sheet can be derived by finding a solution of the wave equation for SH waves which satisfies appropriate boundary conditions. It is convenient and instructive, however, to derive the characteristic equation geometrically, for this method offers a clear physical picture of its origin. SH waves incident on a free surface or a liquid inter¬ face are completely reflected without a change of phase (see for example Jeffreys (1926)). Consequently a floating ice sheet be¬ haves essentially as a wave guide for the propagation of SH waves.

the indicated differentiation one obtains U- - 4l/c (^) (20)

U/A and c//3, are plotted for the first and second modes as

functions of the dimensionless parameter \jjl-: H-f/vj in

Figure 2. The higher modes of Love waves are simply higher har¬ monics of the first or fundamental mode. The sequence of waves arriving at a given point from a distant disturbance can be described with the aid of the group velocity curve of Figure 2, The first arrivals are high frequency waves which travel with the velocity • As time progresses the frequency of the arrivals decreases. This corresponds to moving down the group velocity curve. The wave train is infinitely long, the last wave having the lowest frequency given by

REFERENCES

Lamb, Horace, On elastic waves in a plate, Proc. Roy. Soc. Lond. A 93, p. 114, 1917. Stoneley, Robert, The elastic waves at the surface of separation of two solids, Proc. Roy. Soc. Lond. A 106, p. 416-428,

Jeffreys, Harold, The reflection and refraction of elastic waves, Mon. Not. Roy. Astron. Soc., Geoph. SuddI., vol. 1, pp. 282-292, 1925. Ewing, Maurice, Crary, A. P., and Thorne Jr., A. M,, Propagation of elastic waves in ice I, Physics, Vol. 5, pp. 165- 1934# Ewing, Maurice, and Crary, A. P., Propagation of elastic waves in ice II, Physics, Vol. 5, pp. I 8 I-I 84 , 1934. Osborne, M. F. M., and Hart, S. D., Transmission, reflection, and guiding of an exponential pulse by a steel plate in water, I, Theory, Journ. Acoust. Soc. Amer., Vol. 17, pp. 1-18, 1945. Press, Frank,coupled Crary, flexural A. P., wavesOliver, in Jack,floating and ice.Katz, Geophysical Samuel, Air- Research Paper No. 6, Air Force Cambridge Research Labs

Press, Frank, and Ewing, Maurice, Theory of Air-coupled flexural waves. Geophysical Research Paper No. 6, Air Force Cambridge Research Labs, 1950.

ct WATER

$>|o