Download Planning Based on Model Checking - Automated Planning - Lecture Slides and more Slides Computer Science in PDF only on Docsity!
Chapter 17
Planning Based on Model Checking
Lecture slides for
Automated Planning: Theory and Practice
Motivation
- Actions with multiple possible
outcomes
- Action failures
- e.g., gripper drops its load
- Exogenous events
- Nondeterministic systems are like
Markov Decision Processes (MDPs), but without probabilities attached to the outcomes
- Useful if accurate probabilities aren’t available, or if probability calculations would introduce inaccuracies
a
c b
grasp(c)
a
c
b Intended outcome
a b Unintended outcome
Goal
Start
2
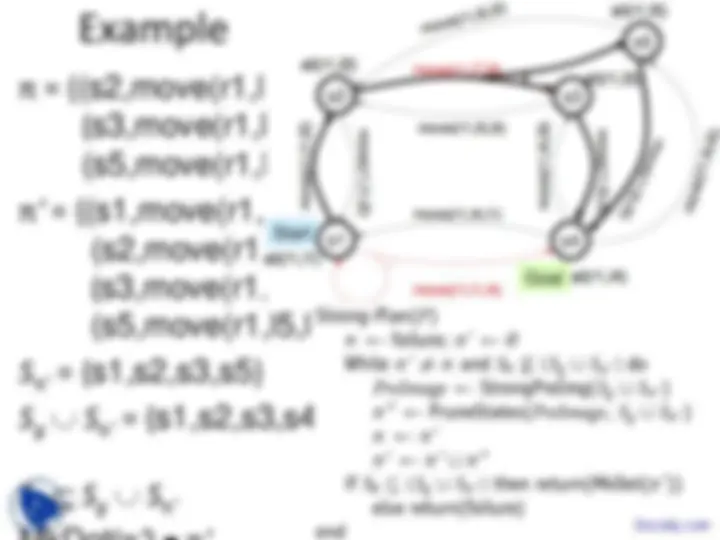
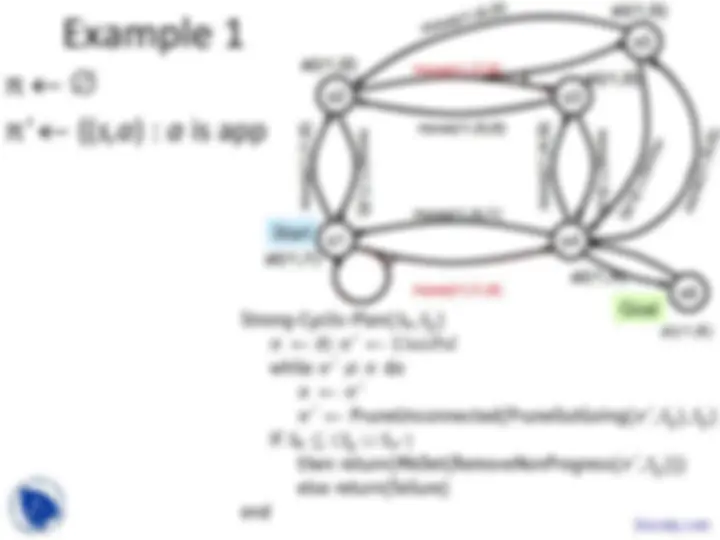
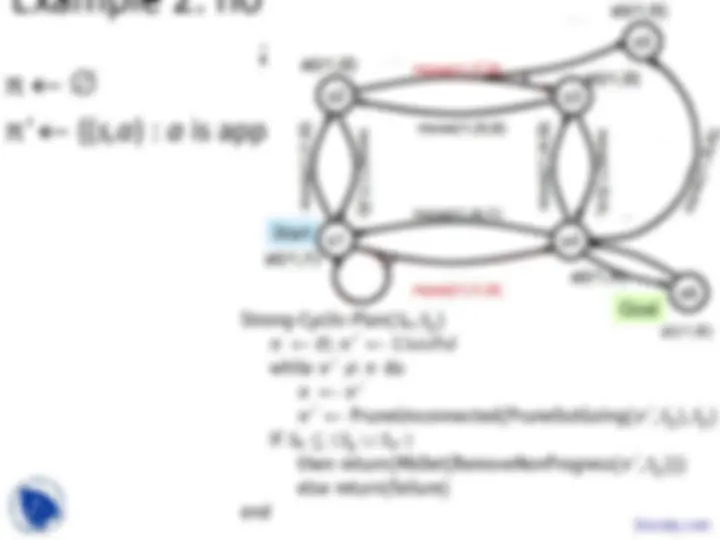
Example
- Robot r1 starts at location l
- Objective is to get r1 to location l
- π 1 = {(s1, move(r1,l1,l2)), (s2, move(r1,l2,l3)), (s3, move(r1,l3,l4))}
- π 2 = {(s1, move(r1,l1,l2)), (s2, move(r1,l2,l3)), (s3, move(r1,l3,l4)), (s5, move(r1,l3,l4))}
- π 3 = {(s1, move(r1,l1,l4))}
Goal
Start
2
Example
- Robot r1 starts at location l
- Objective is to get r1 to location l
- π 1 = {(s1, move(r1,l1,l2)), (s2, move(r1,l2,l3)), (s3, move(r1,l3,l4))}
- π 2 = {(s1, move(r1,l1,l2)), (s2, move(r1,l2,l3)), (s3, move(r1,l3,l4)), (s5, move(r1,l3,l4))}
- π 3 = {(s1, move(r1,l1,l4))}
Goal
Start
2
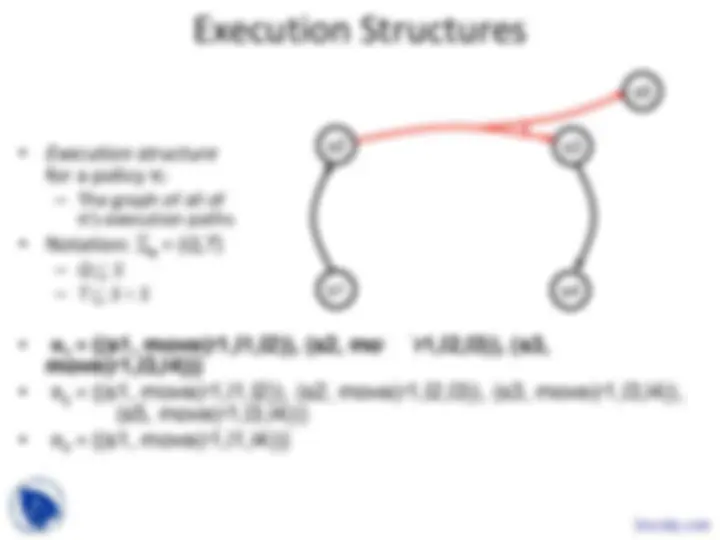
Execution Structures
- Execution structure for a policy π: - The graph of all of π’s execution paths
- Notation: Σπ = ( Q , T )
- π 1 = {(s1, move(r1,l1,l2)), (s2, move(r1,l2,l3)), (s3, move(r1,l3,l4))}
- π 2 = {(s1, move(r1,l1,l2)), (s2, move(r1,l2,l3)), (s3, move(r1,l3,l4)), (s5, move(r1,l3,l4))}
- π 3 = {(s1, move(r1,l1,l4))}
s
s
s
s
s
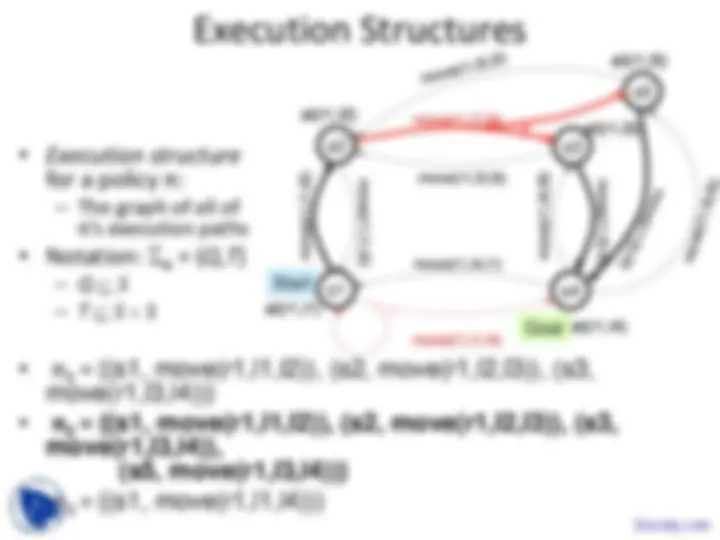
Execution Structures
- Execution structure for a policy π: - The graph of all of π’s execution paths
- Notation: Σπ = ( Q , T )
- π 1 = {(s1, move(r1,l1,l2)), (s2, move(r1,l2,l3)), (s3, move(r1,l3,l4))}
- π 2 = {(s1, move(r1,l1,l2)), (s2, move(r1,l2,l3)), (s3, move(r1,l3,l4)), (s5, move(r1,l3,l4))}
- π 3 = {(s1, move(r1,l1,l4))}
s
s
s
s
s
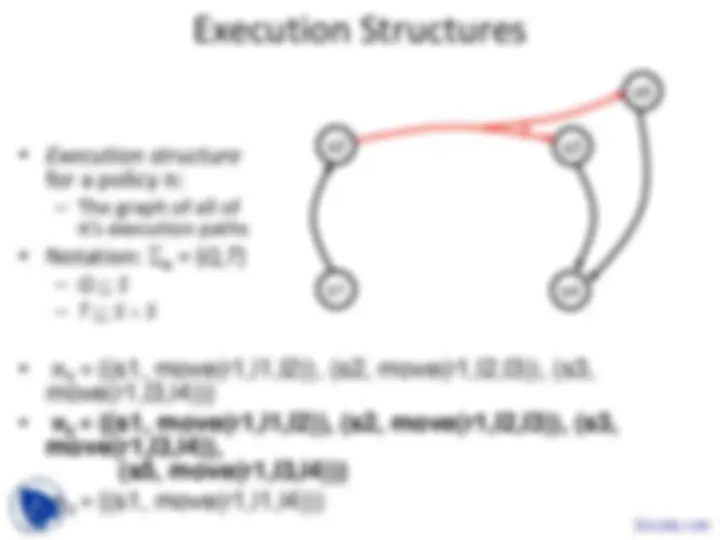
Execution Structures
for a policy π:
- The graph of all of π’s execution paths
- Notation: Σπ = ( Q , T )
- Q ⊆ S
- T ⊆ S × S
- π 1 = {(s1, move(r1,l1,l2)), (s2, move(r1,l2,l3)), (s3,
move(r1,l3,l4))}
- π 2 = {(s1, move(r1,l1,l2)), (s2, move(r1,l2,l3)), (s3,
move(r1,l3,l4)), (s5, move(r1,l3,l4))}
- π 3 = {(s1, move(r1,l1,l4))}
s
s
s
s
s
Goal
Start
2
Execution Structures
for a policy π:
- The graph of all of π’s execution paths
- Notation: Σπ = ( Q , T )
- Q ⊆ S
- T ⊆ S × S
- π 1 = {(s1, move(r1,l1,l2)), (s2, move(r1,l2,l3)), (s3,
move(r1,l3,l4))}
- π 2 = {(s1, move(r1,l1,l2)), (s2, move(r1,l2,l3)), (s3,
move(r1,l3,l4)), (s5, move(r1,l3,l4))}
- π 3 = {(s1, move(r1,l1,l4))}
s1 (^) s
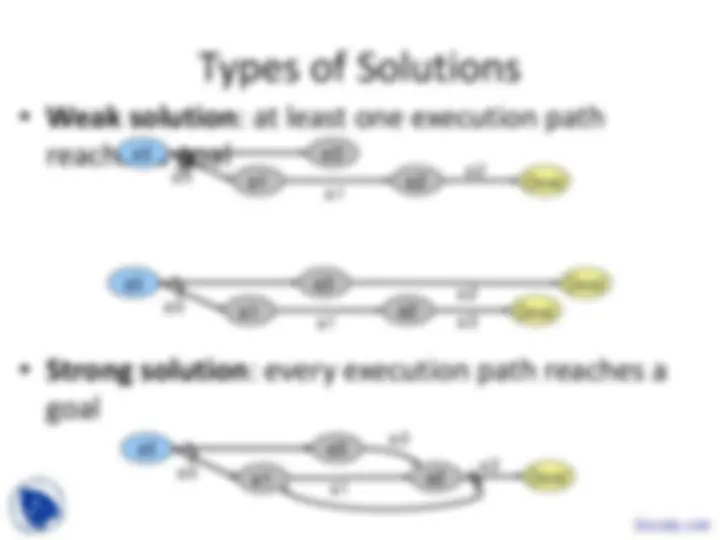
Types of Solutions
• Weak solution : at least one execution path
reaches a goal
• Strong solution : every execution path reaches a
goal
s s
s a0 Goal a
a s
a
s s
s a0 Goal a
a s
s s
s a0 a1 Goal
a s
Goal
a
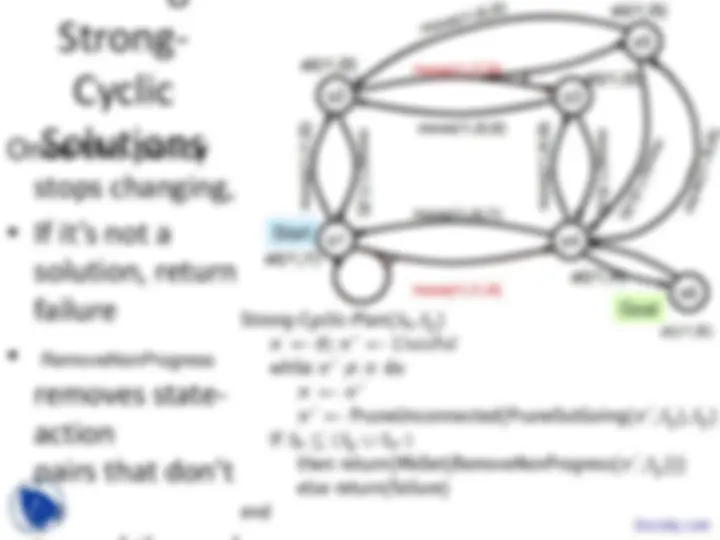
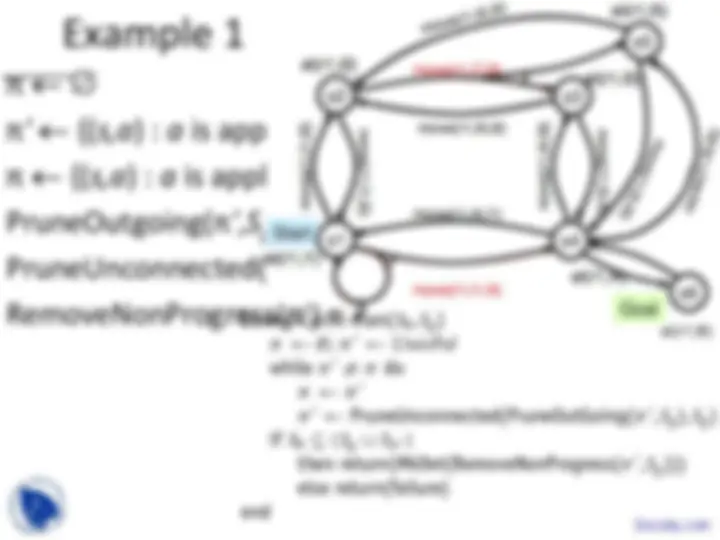
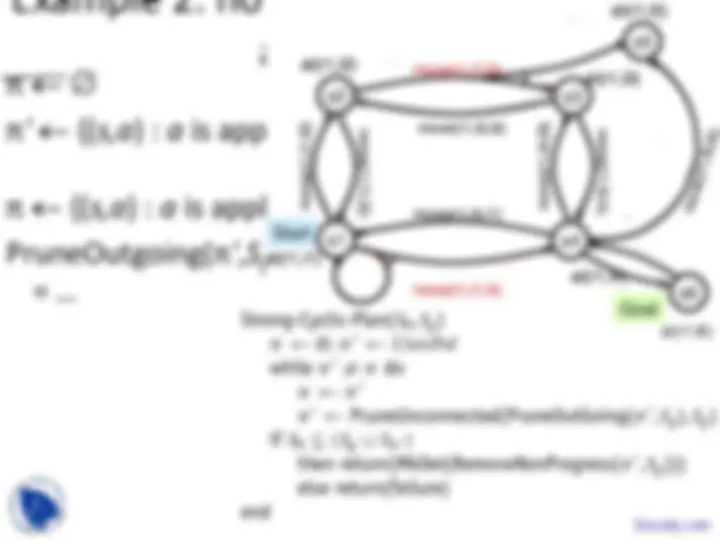
Finding Strong Solutions
• Backward breadth-first search
• StrongPreImg( S )
= {( s,a ) : γ( s,a ) ≠ ∅, γ( s,a ) ⊆ S }
– all state-action pairs for which
all of the successors are in S
• PruneStates(π, S )
= {( s,a ) ∈ π : s ∉ S }
– S is the set of states we’ve
already solved
– keep only the state-action
pairs for other states
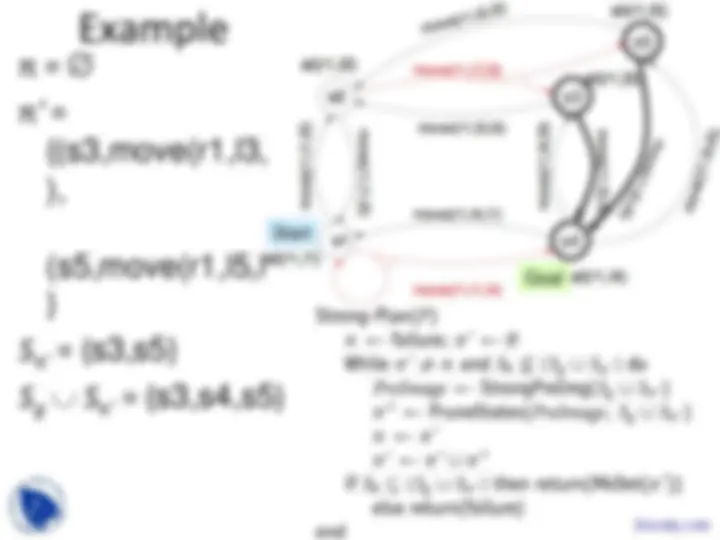
Start
Example
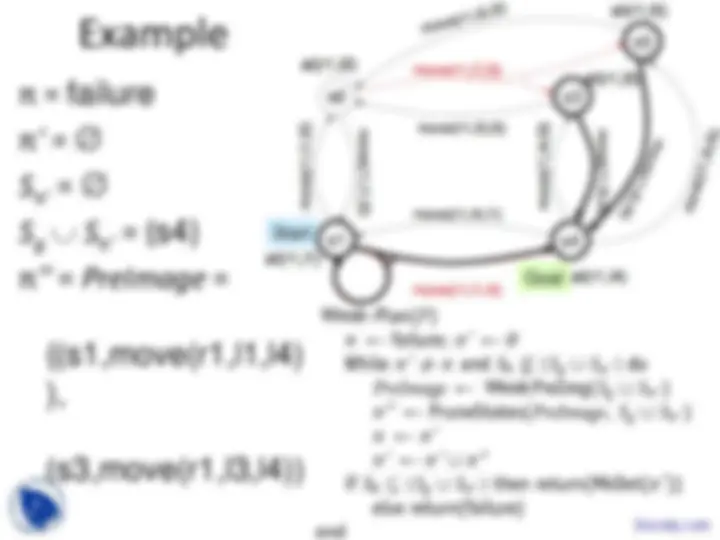
π = failure
S π ' = ∅
S g ∪ S π ' = {s4}
π '' ← PreImage =
{(s3,move(r1,l3,l
(s5,move(r1,l5,l
Goal
s
s
s
2
Start
Example
π = failure
S π ' = ∅
S g ∪ S π ' = {s4}
π '' ← PreImage =
{(s3,move(r1,l3,l4)
(s5,move(r1,l5,l4))
Goal
s
s
s
2
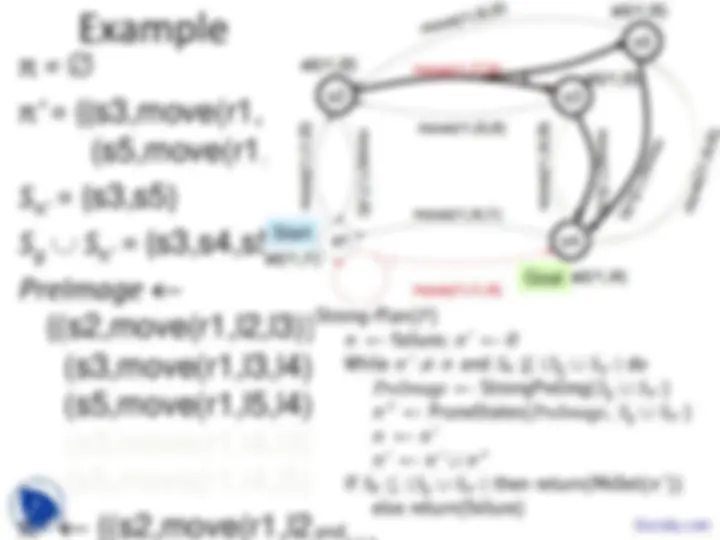
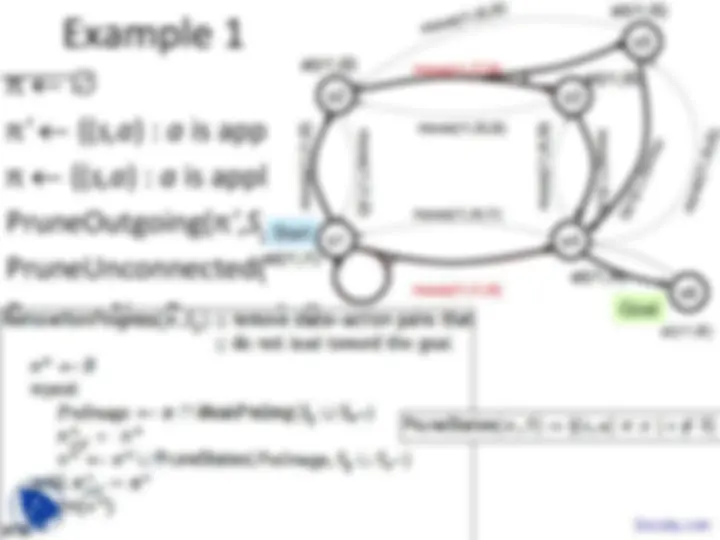
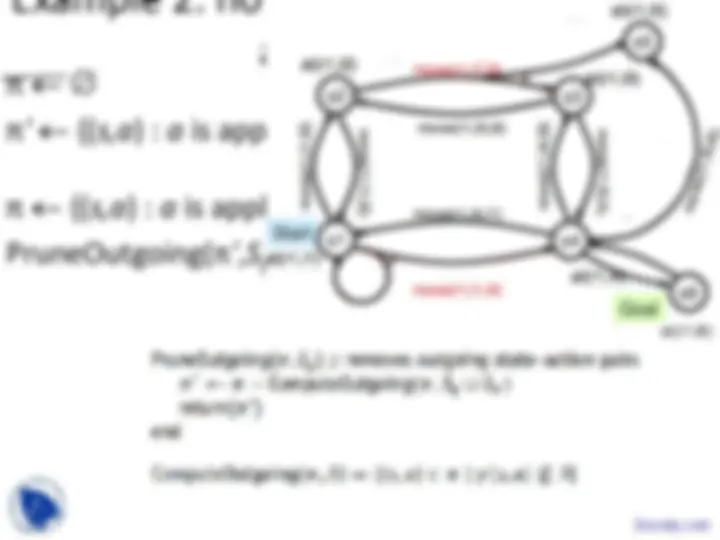
Example
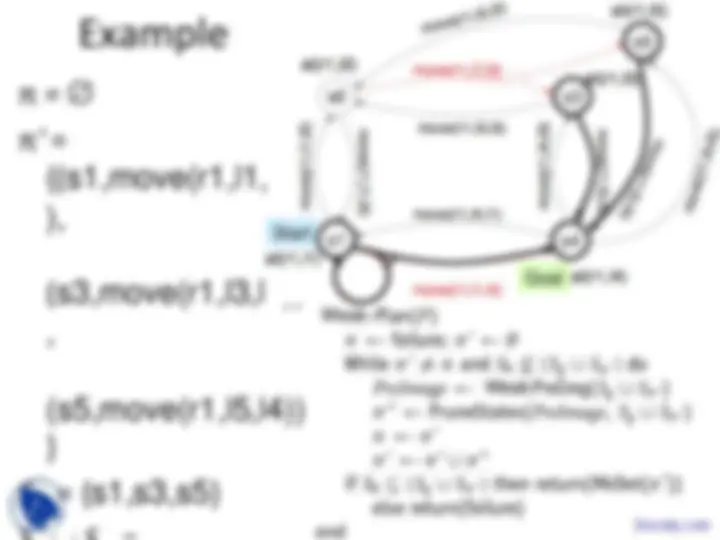
π ' = {(s3,move(r1,l3,l4)),
(s5,move(r1,l5,l4))}
S π ' = {s3,s5}
S g ∪ S π ' = {s3,s4,s5}
PreImage ←
{(s2,move(r1,l2,l3)),
(s3,move(r1,l3,l4)),
(s5,move(r1,l5,l4)),
(s3,move(r1,l4,l3)),
(s5,move(r1,l4,l5))}
π '' ← {(s2,move(r1,l2,l3))}
Goal
Start
s
s
s
s
2
Docsity.com
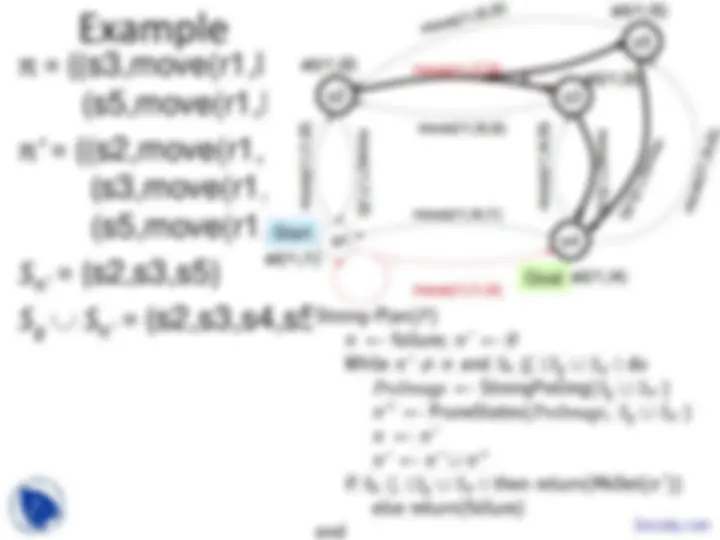
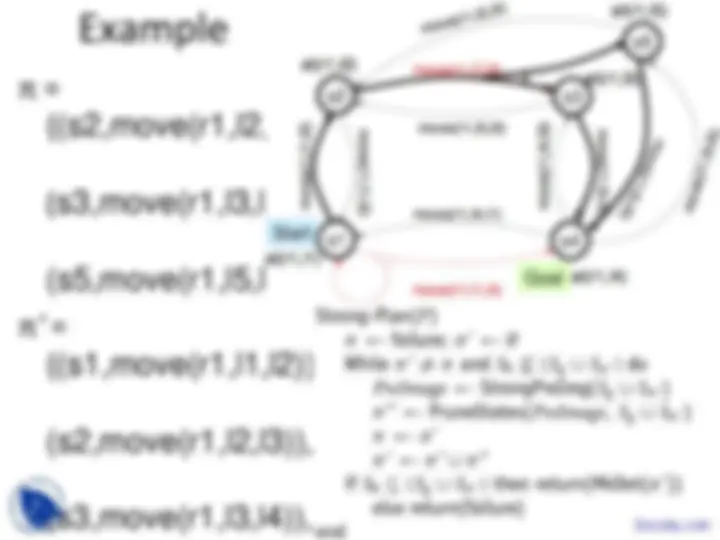
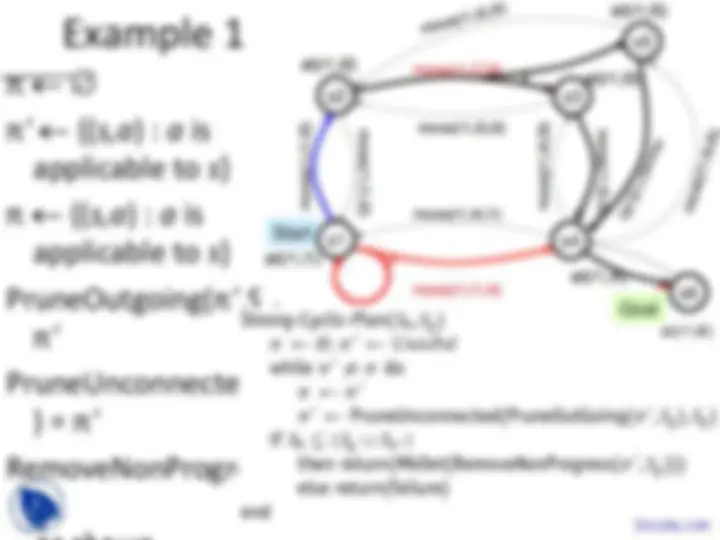
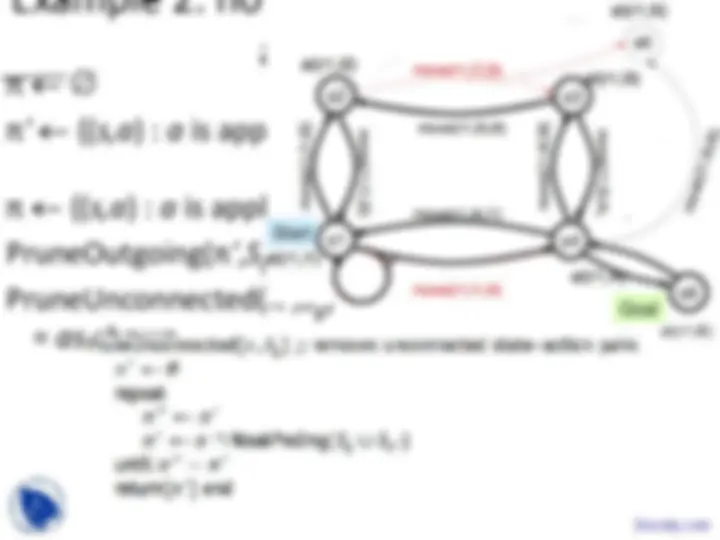
Example
π = {(s3,move(r1,l3,l4)),
(s5,move(r1,l5,l4))}
π ' = {(s2,move(r1,l2,l3)),
(s3,move(r1,l3,l4)),
(s5,move(r1,l5,l4))}
S π ' = {s2,s3,s5}
S g ∪ S π ' = {s2,s3,s4,s5}
Goal
Start
s
s
s
s
2