









Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
Lecture slides on plan-space planning (psp), a technique used in automated planning to overcome the limitations of state-space search. Psp is a forward-chaining, goal-driven planning method that searches for a partially ordered plan to achieve a goal. It involves identifying open goals and threats, and resolving them through the use of causal links and constraints. Examples and explanations of the psp algorithm and its advantages.
Typology: Slides
1 / 21

This page cannot be seen from the preview
Don't miss anything!














Motivation
orderings, instantiations, etc., until necessary
a b c b a
b a^ b a c b c (^) a c b
goal
dead end dead end
dead end dead end dead end dead end
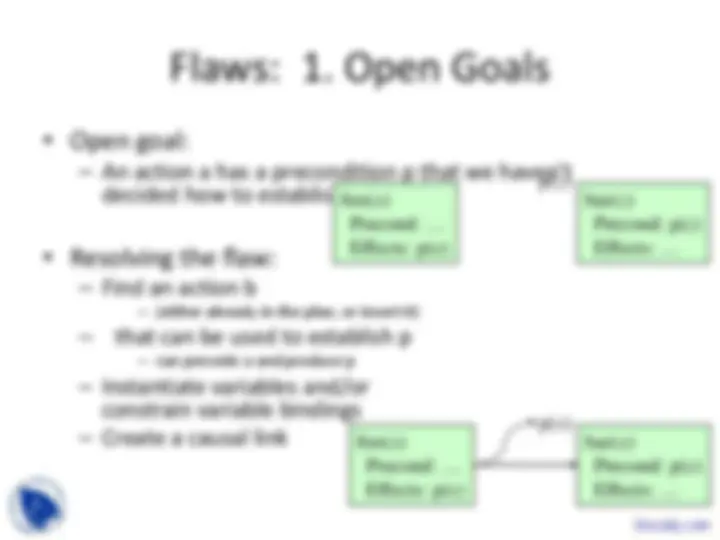
foo( x ) Precond: … Effects: p( x )
bar(y) Precond: ¬p( y ) Effects: …
baz( z ) Precond: p( z ) Effects: …
p( z )
x ≠ y
x = z
foo( x ) Precond: … Effects: p( x )
baz( z ) Precond: p( z ) Effects: …
p( z )
foo( x ) Precond: … Effects: p( x )
baz( x ) Precond: p( x ) Effects: …
p( x )
Example
Start and Finish are dummy actions that we’ll use instead of the initial state and goal
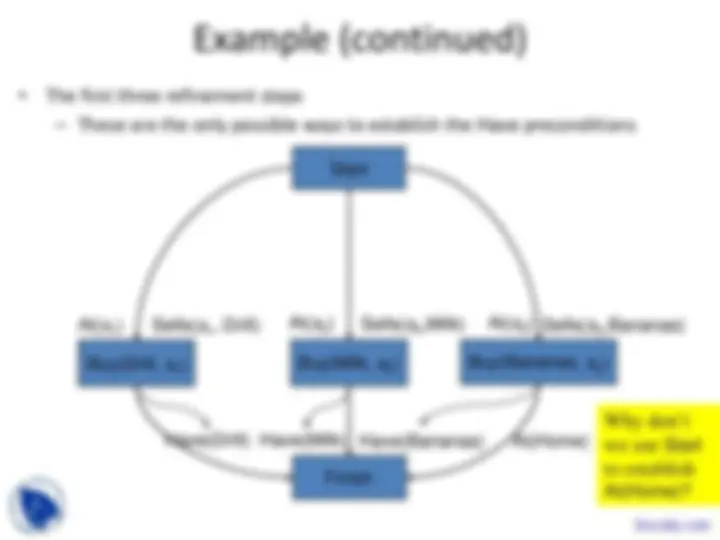
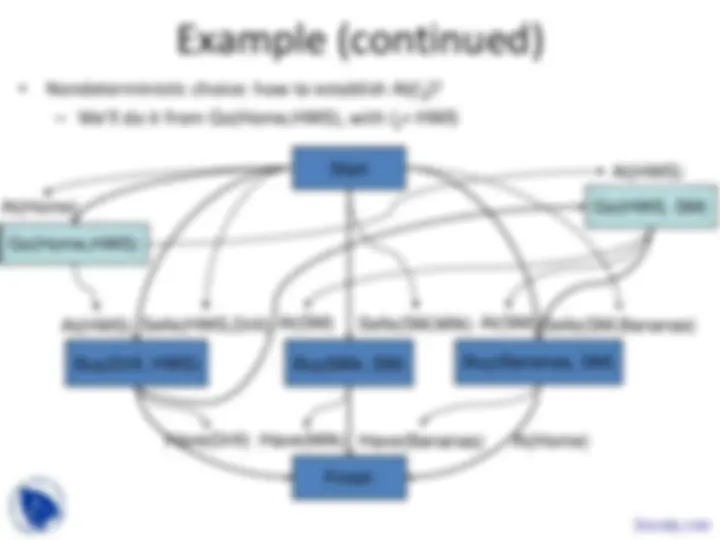
Example (continued)
At( s 1 ) At( s 2 )^ At( s 3 )
Buy(Drill, s 1 ) Buy(Milk, s 2 ) Buy(Bananas,^ s 2 )
Have(Drill)
Start
Buy(Drill, s 1 )
Finish
Have(Milk) (^) Have(Bananas)
Sells( s 1 , Drill) Sells( s 2 ,Milk)^ Sells( s 3 ,Bananas)
At(Home)
Why don’t we use Start to establish At(Home)?
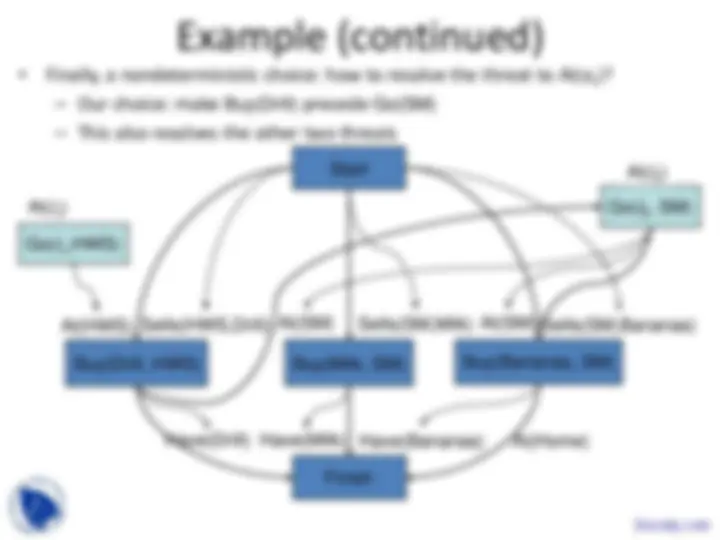
Example (continued)
At(HWS) At(SM)^ At(SM)
Buy(Drill, s 1 ) (^) Buy(Milk, SM) Buy(Bananas, SM)
Have(Drill)
Start
Buy(Drill, HWS)
Finish
Have(Milk) (^) Have(Bananas)
Sells(HWS,Drill) Sells(SM,Milk)^ Sells(SM,Bananas)
At(Home)
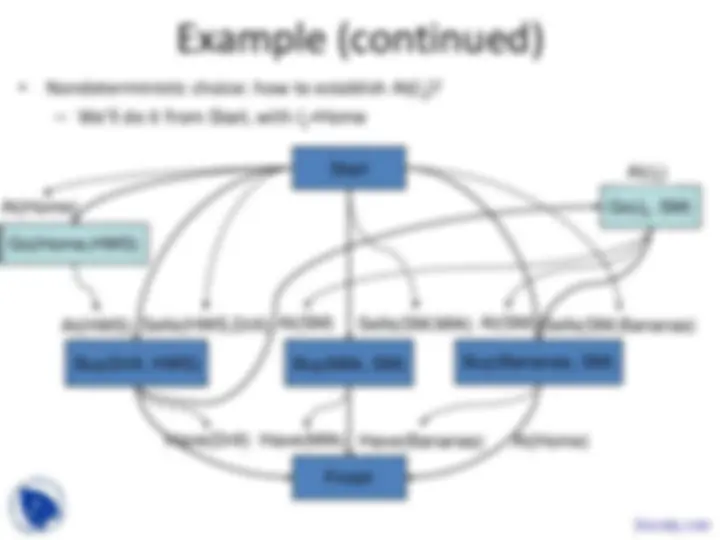
At(SM)
Buy(Drill, s 1 )
Have(Drill)
Start
Finish
Have(Milk) (^) Have(Bananas)
Sells(SM,Milk) (^) Sells(SM,Bananas)
Go( l 2 , SM)
At(Home)
At( l 2 ) At( l 1 )
Go( l 1 ,HWS)
At(HWS) Sells(HWS,Drill) At(SM)
Buy(Drill, HWS) Buy(Milk, SM) Buy(Bananas, SM)
At(Home)
At(SM)
Buy(Drill, s 1 )
Have(Drill)
Start
Finish
Have(Milk) (^) Have(Bananas)
Sells(SM,Milk) (^) Sells(SM,Bananas)
Go( l 2 , SM)
Go(Home,HWS)
At(Home)
At( l 2 )
At(HWS) Sells(HWS,Drill) At(SM)
Buy(Drill, HWS) Buy(Milk, SM) Buy(Bananas, SM)
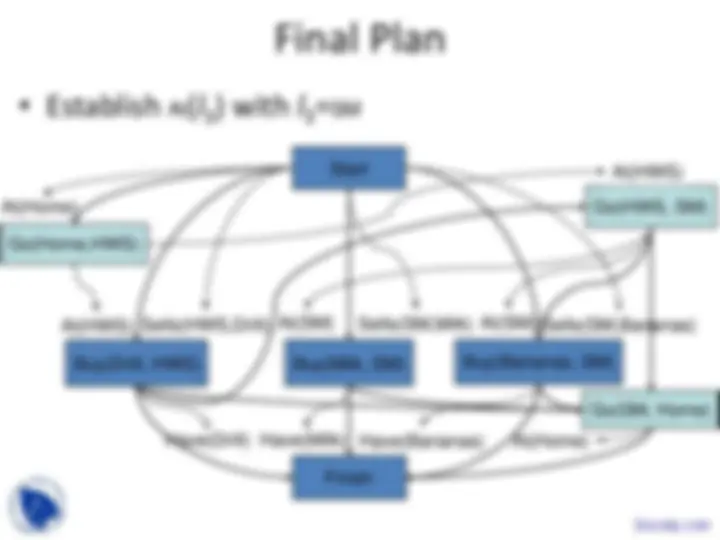
Go( l 3 , Home)
At(Home)
At(SM)
Buy(Drill, s 1 )
Have(Drill)
Start
Finish
Have(Milk) (^) Have(Bananas)
Sells(SM,Milk) (^) Sells(SM,Bananas)
Go(HWS, SM)
Go(Home,HWS)
At(Home)
At(HWS)
At(HWS) Sells(HWS,Drill) At(SM)
Buy(Drill, HWS) Buy(Milk, SM) Buy(Bananas, SM)
Go( l 3 , Home)
At(Home)
At(SM)
Buy(Drill, s 1 )
Have(Drill)
Start
Finish
Have(Milk) (^) Have(Bananas)
Sells(SM,Milk) (^) Sells(SM,Bananas)
Go(HWS, SM)
Go(Home,HWS)
At(Home)
At(HWS)
At(HWS) Sells(HWS,Drill) At(SM)
Buy(Drill, HWS) Buy(Milk, SM) Buy(Bananas, SM)
a b c b a
b a^ b a c b c (^) a c b
goal
s 0 = { d 3 =0, d 2 =0, d 1 =0} g = { d 3 =1, d 2 =1, d 1 =0}
incr Precond: d 1 = Effects: d 1 =
incr Precond: d 2 =0, d 1 = Effects: d 2 =1, d 1 =
incr Precond: d 3 =0, d 2 =1, d 1 = Effects: d 3 =1, d 2 =0, d 1 =0 Docsity.com