Optimisation of functions of several variables Unconstrained Optimisation, Slides of Econometrics and Mathematical Economics

Download Optimisation of functions of several variables Unconstrained Optimisation and more Slides Econometrics and Mathematical Economics in PDF only on Docsity!

1

Optimisation of functions of

several variables

Unconstrained Optimisation 2

Recall……

Max Min X Y

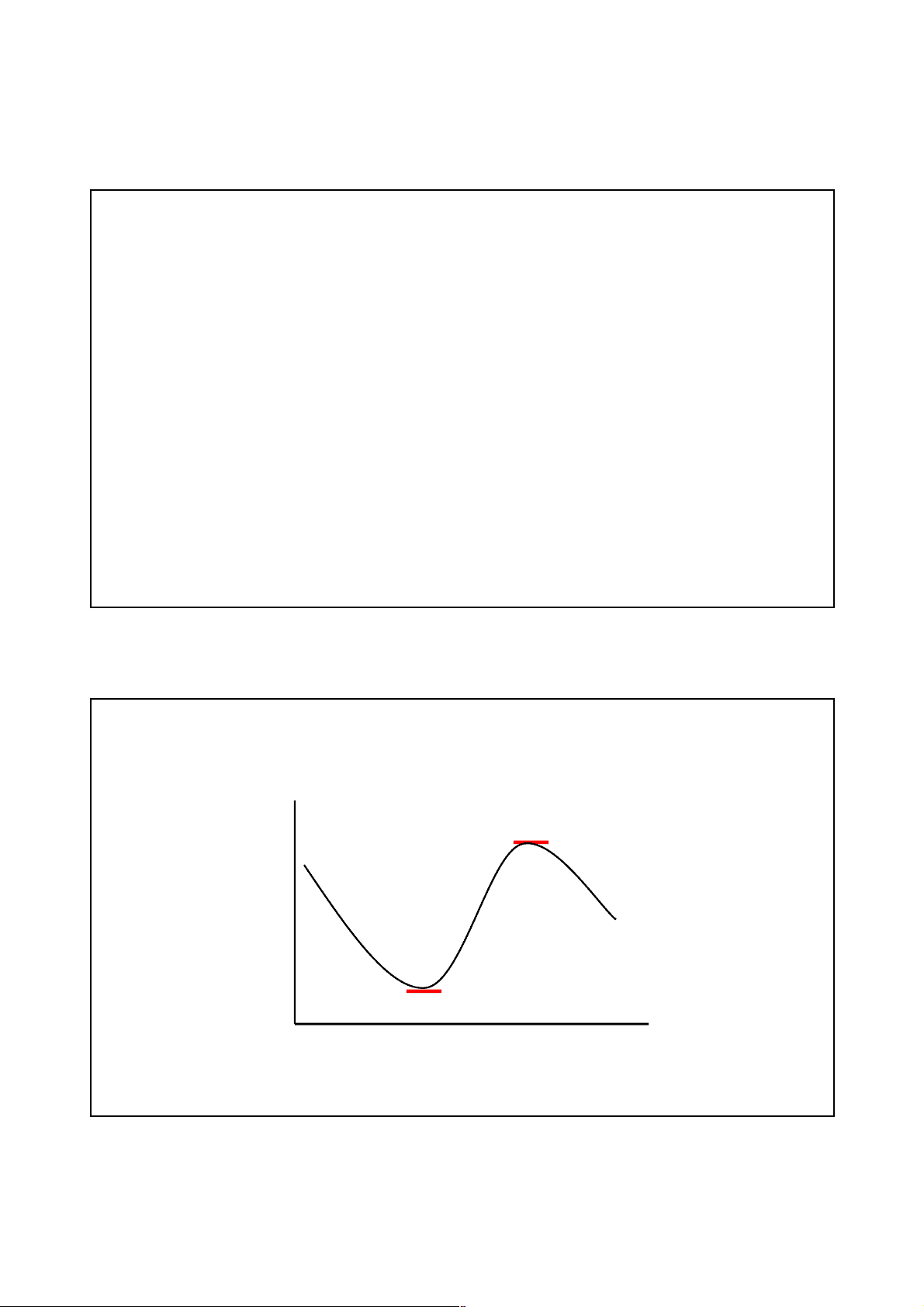
3 First-Order / Necessary Condition:

dY/dX = f ¢ (X) = 0

Second-Order / Sufficent Condition:

d

2

Y/dX

2

= f ¢¢(X) if > 0 (Min)

if < 0 (Max)

Max Y = f (X) X* 4

Re-writing in terms of total differentials….Max Y = f (X)

X* Necessary Condition: dY = f ¢ (X).dX = 0 , so it must be that f ¢(X)= 0 Sufficent Condition: d^2 Y = f ¢¢ (X).dX^2 >0 for Min <0 for Max For Positive Definite, (Min ), it must be that f ¢¢ > 0 Negative Definite, (Max), it must be that f ¢¢ < 0

7 d 2 Y= fXX.dX 2

• fZZ.dZ 2
• 2fXZ dX.dZ Complete the Square (^22) 2 (^2) dZ f dZ f f^ f f dY f dX^ f XX XX ZZ XZ XX XX XZ ú ú û ù ê ê ë é (^) - ú^ + û ù ê ë =^ é^ + Sign Positive Definite To ensure d^2 Y > 0 and Min: fXX > 0 and fXXfZZ - fXZfZX > 0 Sign Negative Definite To ensure d^2 Y < 0 and Max: fXX < 0 and fXXfZZ - fXZfZX > 0 note: fXZ.fZX = (fXZ)^2 8 Optimisation - A summing Up… Condition Y = f(X) Y = f(X,Z) Neccesary So required that……. dY = 0 fX = 0 dY = 0 fX = 0 AND fZ = 0 Sufficient For Min So required that ….. d^2 Y > 0 fXX > d^2 Y > 0 fXX > 0 AND fXX fZZ – (fXZ)^2 > Sufficient For Max So required that ….. d^2 Y < 0 fXX < 0 d^2 Y < 0 fXX < 0 AND fXX fZZ – (fXZ) 2

fXX fZZ – (fXZ) 2 < Saddle Point

9 Examples Find all the maximum and minimum values of the functions: (i) y^^10 20 x^2 x^16 z z^2 xz = + -^2 + -^2 - Necessary Condition for max or min:

1. fx =^20 -^4 x -^2 z =^0 and
2. fz =^16 -^2 z -^2 x =^0 Solve simultaneously
   • 2 z = 4 x - 20
   • 2 z = 2 x - 16 So 4 x -^20 =^2 x -^16 x = 2 Subbing in x = 2 to eq. 1 (or 2):
   • 2 z =- (^12) and z = 6 There is 1 stationary point at (2,6) 10 Second Order Conditions: fxx =- 4 < 0 fzz =- 2 < 0 fxz =- 2 Thus, fXX fZZ – (fXZ) 2 = (-4.-2) – (-2) 2 = +8 – 4 = +4 > Sufficient condition for Max ( d 2 Y < 0). fxx < 0 and fXX fZZ – (fXZ) 2

So, Max at (2,6)

13

Example 3

(iii) z z y x^ x 2 5 2 20 2 2 = - + - Necessary Condition for max or min:

1. f^ x =^20 - x =^0 and
2. fz =^4 z -^5 =^0 Thus, x^ =^20 and z =^54 There is 1 stationary point at (^20 ,^54 ) Second Order Conditions fxx =- 1 < 0 fzz = 4 > 0 fxz = 0 fXX fZZ – (fXZ)^2 = (-1.4) – (0^2 ) = - 4 < 0 Since, fxx < 0 and fXX fZZ – (fXZ)^2 <0, Saddle Point at (^20 ,^54 ) 14

Optimisation of functions of several variables

Economic Applications

15

Example 1

A firm can sell its product in two countries, A and B, where demand in country A is given by PA = 100 – 2QA and in country B is PB = 100 – QB. It’s total output is QA + QB, which it can produce at a cost of TC = 50(QA+QB) + ½ (QA+QB)^2 How much will it sell in the two countries assuming it maximises profits? 16

Objective Function to Max is Profit….

P = TR - TC = PAQA + PBQB – TC PAQA = ( 100 – 2 QA)QA PBQB = ( 100 – QB) QB P = 100 QA – 2 QA^2 + 100 QB – QB^2

• 50 QA – 50 QB – ½ (QA+QB)^2 = 50 QA – 2 QA^2 + 50 QB – QB^2 – ½ (QA+QB)^2 Select QA and QB to max P :

19

Example 2

Profits and production Max p = PQ(L, K) – wL - rK {L, K} Total Revenue = PQ Expenditure on labour L = wL Expenditure on Capital K = rK Find the values of L & K that max p 20 Necessary Condition: dp = 0 pL = PQL – w = 0 , MPL = QL = w/P pK = PQK – r = 0 , MPK = QK = r/P Sufficient Condition for a max, d^2 p < So pLL < 0 AND (pLL.pKK - pLK.pKL) > 0

21 Max p = 2 K1/3L1/2^ – L – 1/3 K {L, K}

Necessary condition for Max: d p =

(1) pL = K1/3L-1/2^ – 1 = 0 (2) pK = 2 / 3 K-2/3^ L1/2^ – 1 / 3 = 0 Stationary point at [L, K] = [4, 8] note: to solve, from eq1: L½^ = K1/3^. Substituting into eq2 then, (^2) / 3 K– 2/3K1/3 (^) = 1 / 3. Re-arranging K– 1/3 (^) = ½ and so K 1/3 (^) = 2 = L½. Thus, K* =2^3 = 8. And so L* = 2^2 = 4. NOW, let Q = K1/3L1/2, P = 2, w = 1, r =1/ Find the values of L & K that max p? 22 pL = K1/3L-1/2^ – 1 pK = 2 / 3 K-2/3^ L1/2^ – 1 / 3 pLL = -^1 / 2 K1/3L-3/2^ < 0 for all K and L pKK = – 4 / 9 K–5/3L½ pKL = pLK = 1 / 3 K–2/3L-½ For sufficient condition for a max, Check d^2 p <0; p LL < 0 & ( p LL. p KK - p LK. p KL)>