Download Shortest Paths with Multiplicative Costs and Maximum Flow in Networks and more Exams Data Structures and Algorithms in PDF only on Docsity!
Be neat and concise, but complete.
- (10 points). Consider a version of the shortest path problem with multiplicative costs. In this form of the problem, the length of a path is the product of the edge lengths, rather than the sum. Explain how shortest path algorithms can be modified to handle multiplicative costs. What is the implication of having positive edge costs that are less than 1?
One way to do this is to replace the original costs by their logarithms and then use a standard shortest path algorithm on the graph with the transformed costs. The result distances must then be transformed back to give the multiplicative distances. Since the logarithm of a product is equal to the sum of the logarithms, this procedure yields the shortest multiplicative paths. Alternatively, one can modify the original algorithms to replace expressions of the form dist(u) + length(u,v) with dist(u) * length(u,v) in the shortest path algorithm. The correctness of this follows from the logarithm transformation. Positive edge costs less than 1 reduce path lengths and have the same effect as negative edge lengths in the standard problem. If such edges are present, Dijkstra’s algorithm cannot be used.
- (10 points) Increase the flow in the network shown below by finding an augmenting path using the distance labeling algorithm. Whenever there are multiple admissible edges available for extending a path, use the one whose other endpoint comes first in alphabetical order. Be sure to show how the distance labels change, as well as showing the augmenting path found.
CS 541 – Algorithms and Programs
Exam 2 Solutions
Jonathan Turner 11/8/
1
s
f
e
c
t
h g
b
a
d
5,
0
2
3
3
(^2 )
2
4 (^3) 2,
3,
6,5 (^) 7,
7,
8,2 2,
6,2 (^) 5, 2, 3,0 4,
1,
2,
2,
1,
3,
1
s
f
e
c
t
h g
b
a
d
5,
0
2
3
3
(^2 )
2
4 (^3) 2,
3,
6,5 (^) 7,
7,
8,2 2,
6,2 (^) 5, 2, 3,0 4,
1,
2,
2,
1,
3,
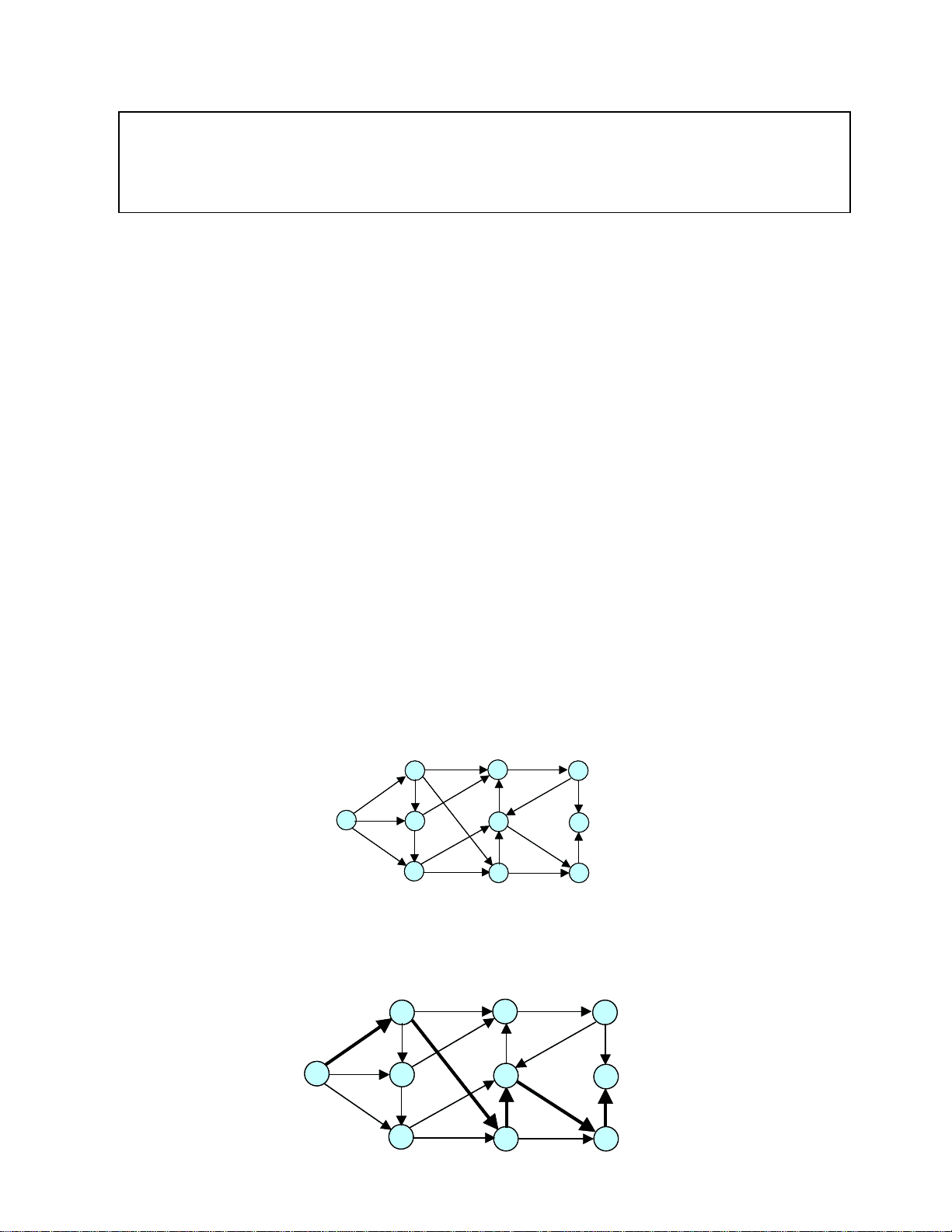
The augmenting path is shown in bold and the modified distance labels are also shown in bold. The augmenting path has a residual capacity of 1.
1
f
e
c
t
h g
b
a
d
5,
0
2
5
(^4) 2,
3,
6,5 (^) 7, 6
7, 3
2, 8, 3
6,2 (^) 5, 2,
3, 1 4,
1,
2,
2,
1, 1
s 3,
1
f
e
c
t
h g
b
a
d
5,
0
2
5
(^4) 2,
3,
6,5 (^) 7, 6
7, 3
2, 8, 3
6,2 (^) 5, 2,
3, 1 4,
1,
2,
2,
1, 1
s 3,
- (15 points) The picture below shows an implementation of a dynamic tree, using linked paths represented by binary search trees. Draw the actual tree that this represents (with vertex costs). Assuming the actual tree is being used in a maximum flow computation, what is the residual capacity of the path from s to t in the actual tree. Which edges become saturated if the maximum possible amount of flow is added to this path?
4,
∆ min , ∆ cost
b d t
e c
a
1,0 0,
3,0 0,0 (^) 96,
n
g
m (^) 3,
0,
4,
i
s f h
k
2,
5,
3,
1,0 0,
4,
∆ min , ∆ cost
b d t
e c
a
1,0 0,
b (^) 3,0 d 0,0 t 96,
e c
a
b d t
e c
a
1,0 0,
3,0 0,0 (^) 96,
n
g
m (^) 3,
0,
4,
i
s f h
k
2,
5,
3,
1,0 0,
The actual tree appears at right. The edge from d to c is the only one that becomes saturated after 4 units of flow are added to the path skfebadct.
b
t
d
e
c
a
6
f
s
k
g^4
5
5
6
5
6
8
103
4
i
h
5
2
n
m
3
7
b
t
d
e
c
a
b
t
d
e
c
a
6
f
s
k
gg^44
5
5
6
5
6
8
103
4
i
h
5
2
i
h
5
2
n
m
3
7
n
m
3
7
- (15 points) We have shown that the Dinic’s algorithm with shortest path augmentation takes O ( mn )= O ( n^3 ) time to find a blocking flow in a level graph. Show that it also takes Ω( n^3 ) time in the worst-case, by showing that for some constant C and any value of n , there is a level graph on which Dinic’s algorithm takes at least Cn^3 time.
s (^) t
complete bipartite graph with 2 n /3 vertices and edge capcities all equal to 1.
n − 2 n /3 − 2 vertices and edge capcities equal to n^2.
edge capcities equal to n^2.
edge capcities equal to n^2.
The standard version of Dinic’s algorithm will find n/3 ^2 paths in this level graph and for each path it will retrace the path at the left, meaning
that it will take Ω (n 3 ) time overall. In contrast, the Sleator-Tarjan version
of Dinic’s algorithm will run in O(n 2 log n) time, since it can effectively traverse the long path at left in O(log n) time using the dynamic trees data structure.
s (^) t
complete bipartite graph with 2 n /3 vertices and edge capcities all equal to 1.
n − 2 n /3 − 2 vertices and edge capcities equal to n^2.
edge capcities equal to n^2.
edge capcities equal to n^2.
The standard version of Dinic’s algorithm will find n/3 ^2 paths in this level graph and for each path it will retrace the path at the left, meaning
that it will take Ω (n 3 ) time overall. In contrast, the Sleator-Tarjan version
of Dinic’s algorithm will run in O(n 2 log n) time, since it can effectively traverse the long path at left in O(log n) time using the dynamic trees data structure.
- (10 points) Show that the wave method runs faster on a unit network than on a general network. How does the wave method compare to the standard version of Dinic’s algorithm on unit networks?
From the analysis of Dinic’s algorithm on unit networks, we know that the number of blocking steps required to find a maximum flow is O(n 1/2^ ). This applies to the wave method as well. Since the wave method finds a blocking flow in O(n 2 ) time, the overall running time is O(n 5/2^ ), which is better than the O(n 3 ) for general graphs, but not as good as the O(mn 1/2^ ) that the standard version of Dinic’s algorithm achieves on unit networks.
- (15 points). Consider a data structure that maintains a collection of lists of items, with each item appearing on one list, and that supports the following operations:
concat ( L 1 , L 2 ) Combine the list L 1 with the list L 2.
chop ( x ) Separate the list containing x into two lists, one containing all elements preceding x and one containing x and all elements following it.
reverse ( L ) Reverse the order of the elements in list L.
tail ( L ) Return the last element of the list containing L.
These operations can be implemented efficiently using a self-adjusting binary search tree to represent each list, supplemented with a flip bit at each node. If the sum of the flip bits on the path from a node to the root of the tree is even, then the left subtree of a node x contains items that appear before x in its list and the right subtree contains items that appear after x in its list. If the sum is odd, the left subtree contains items that appear after x in its list and the right subtree contains items that appear before it. Fill in the C++ code needed to implement the reverse, tail and concat operations. You need not show how the rotate operations are modified to handle the flip bits. class listset { int n; // lists defined on items 1..n struct node { int flip; // flip bit item parent; // parent in search tree item lc; // left child item rc; // right child } *vec; // vector of nodes public:... };
item listset::reverse(list L){ vec[L].flip = !vec[L].flip; };
