Minimum Spanning Tree-Algorithm Design and Analysis-Lecture Slides, Slides of Design and Analysis of Algorithms

Download Minimum Spanning Tree-Algorithm Design and Analysis-Lecture Slides and more Slides Design and Analysis of Algorithms in PDF only on Docsity!

Minimum Spanning Tree

Algorithms

Docsity.com

Greedy Algorithms

 Main Concept: Make the best or greedy choice at any

given step.

 Choices are made in sequence such that

» Each individual choice is best according to some limited “short- term” criterion, that is not too expensive to evaluate » Once a choice is made, it cannot be undone!  Even if it becomes evident later that it was a poor choice  Sometimes life is like that 

 The goal is to

» take a sequence of locally optimal actions, hoping to yield a globally optimal solution.

Docsity.com

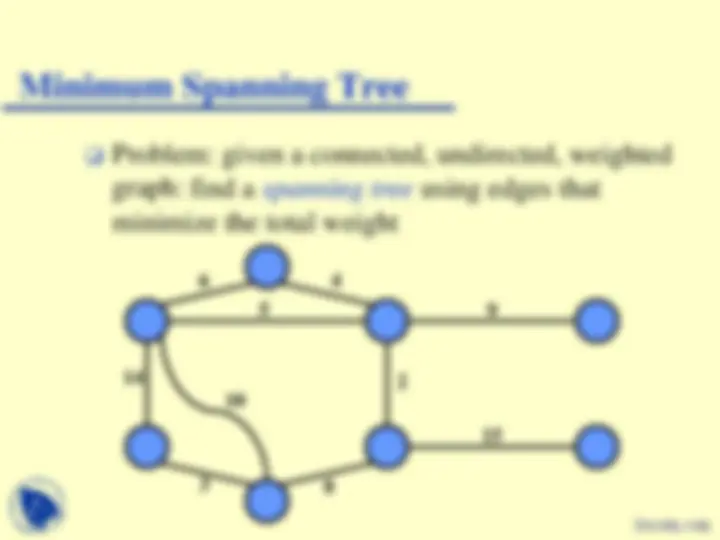
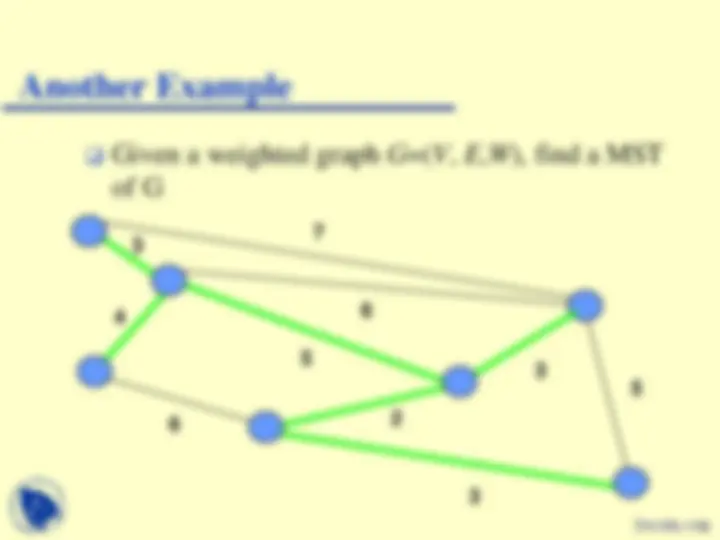
Minimum Spanning Tree (MST)

 A spanning tree for a connected, undirected graph, G =( V , E ) is

1. a connected subgraph of G that forms an

2. undirected tree incident with each vertex.

 In a weighted graph G =( V , E , W ),

» the weight of a subgraph is the sum of the weights of

the edges in the subgraph.

 A minimum spanning tree (MST) for a weighted graph is

» a spanning tree with the minimum weight.

Docsity.com

Minimum Spanning Tree

 Problem: given a connected, undirected, weighted

graph:

find a spanning tree using edges that

minimize the total weight

Docsity.com

Minimum Spanning Tree

 Answer:

H B C

G E D

F

A

Docsity.com

Another Example

 Given a weighted graph G =( V , E , W ), find a MST

of G

Docsity.com

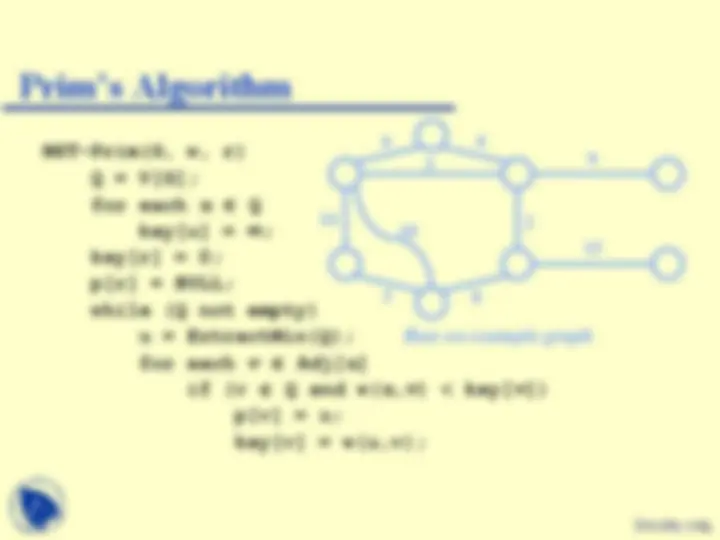
Prime’s Algorithm

(High-Level Pseudocode)

 Prime(G) //Input: A weighted connected graph G = <V, E> //Output: ET --- the set of edges composing MST of G VT = {v 0 } ET =  for i = 1 to |V| - 1 do find a minimum-weight edge e* = (u, v) among all the edges (u, v) such that u is in VT and v is in V-VT VT = VT  {v} ET = ET  {e} return ET

Docsity.com

Prime’s Algorithm

(High-Level Pseudocode)

 Prime(G) //Input: A weighted connected graph G = <V, E> //Output: ET --- the set of edges composing MST of G VT = {v 0 } ET =  for i = 1 to |V| - 1 do find a minimum-weight edge e* = (u, v) among all the edges (u, v) such that u is in VT and v is in V-VT VT = VT  {v} ET = ET  {e} return ET

H B C

G E D

F

A

(^14 )

3

6 4 5

2

9

15

(^8) Docsity.com

Prim’s Algorithm

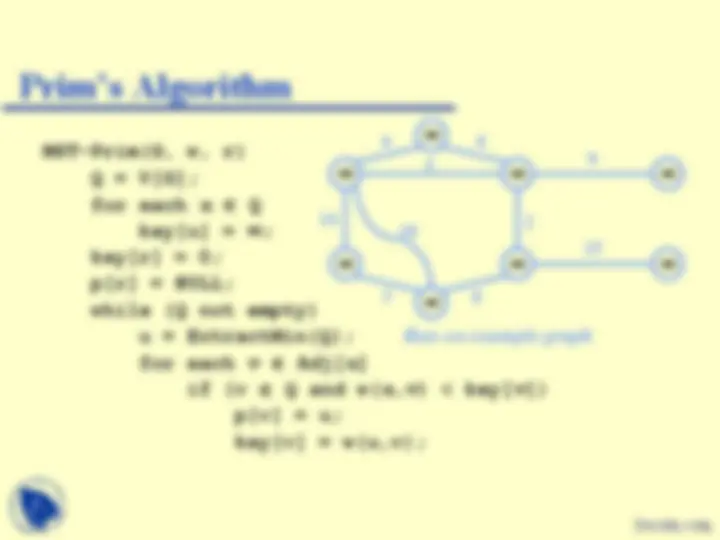
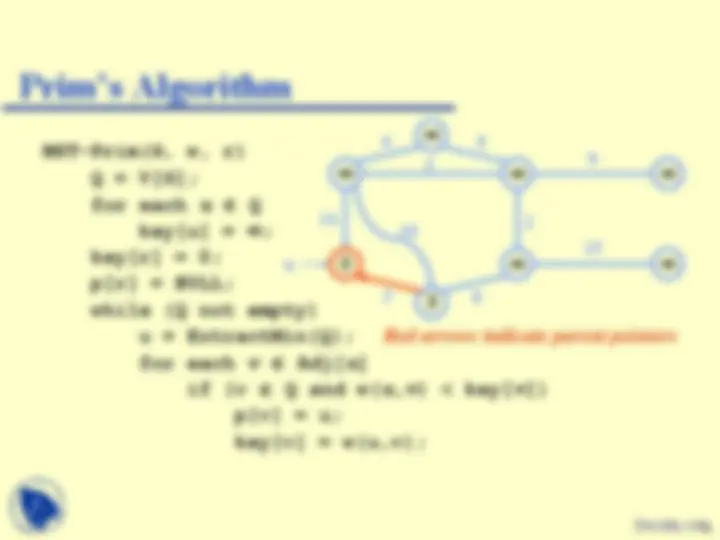
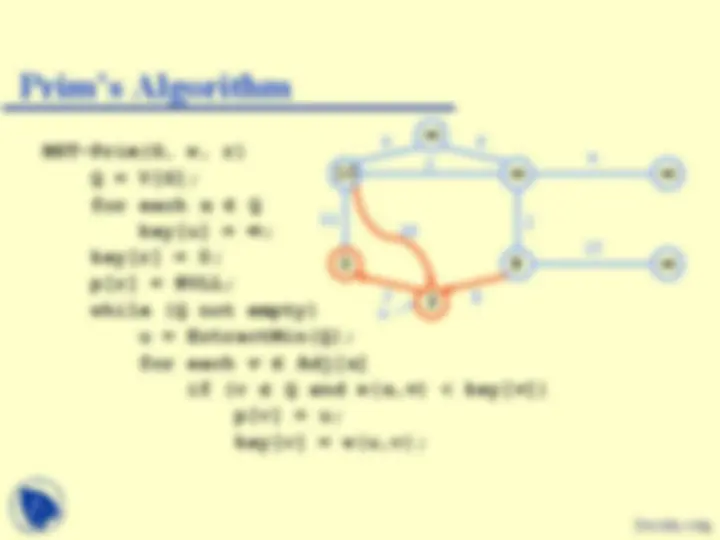
MST-Prim(G, w, r) Q = V[G]; for each u  Q key[u] = ; key[r] = 0; p[r] = NULL; while (Q not empty) u = ExtractMin(Q); for each v  Adj[ u ] if (v  Q and w( u,v ) < key[ v ]) p[v] = u; key[v] = w(u,v);

Grow a single tree by repeatedly

adding the least cost edge that

connects a vertex in the existing tree

to a vertex not in the existing tree

Intermediary solution is a subtree

Docsity.com

Prim’s Algorithm

MST-Prim(G, w, r) Q = V[G]; for each u  Q key[u] = ; key[r] = 0; p[r] = NULL; while (Q not empty) u = ExtractMin(Q); for each v  Adj[ u ] if (v  Q and w( u,v ) < key[ v ]) p[v] = u; key[v] = w(u,v);

14 10

3

6 4 5

2

9

15

8

Run on example graph

Docsity.com

Prim’s Algorithm

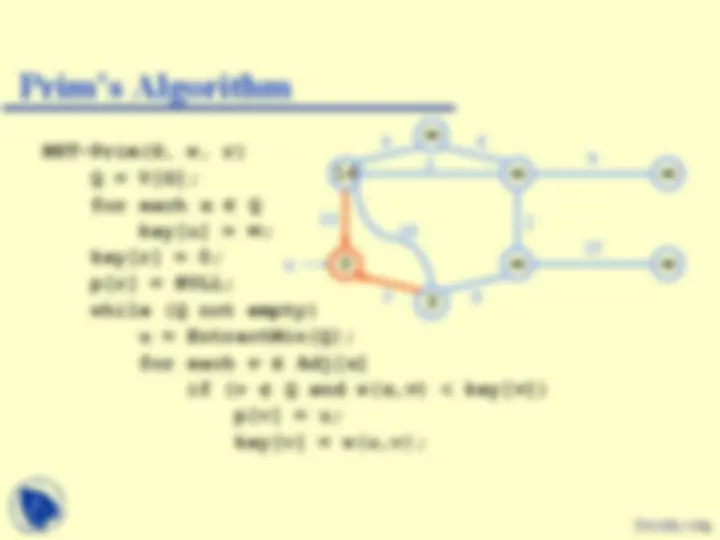
MST-Prim(G, w, r) Q = V[G]; for each u  Q key[u] = ; key[r] = 0; p[r] = NULL; while (Q not empty) u = ExtractMin(Q); for each v  Adj[ u ] if (v  Q and w( u,v ) < key[ v ]) p[v] = u; key[v] = w(u,v);

14 10

3

6 4 5

2

9

15

8

Pick a start vertex r

r

Docsity.com

Prim’s Algorithm

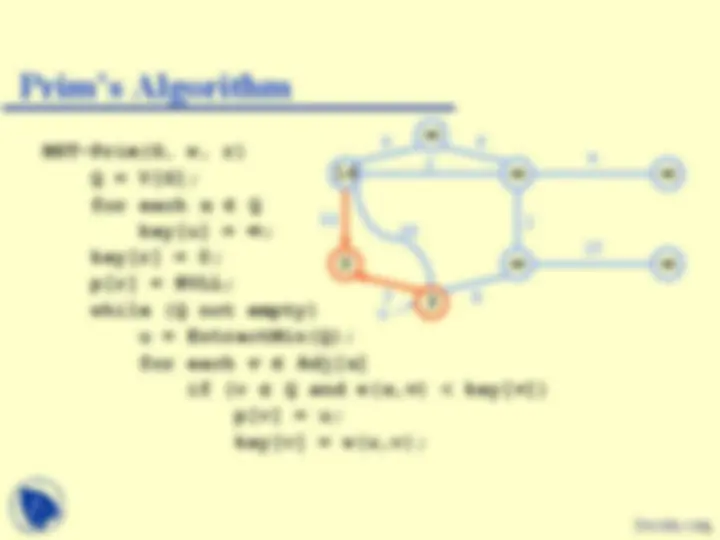
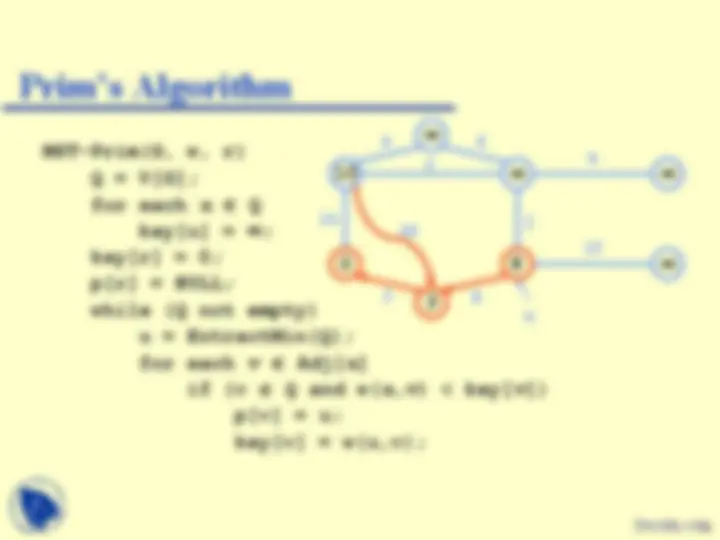
MST-Prim(G, w, r) Q = V[G]; for each u  Q key[u] = ; key[r] = 0; p[r] = NULL; while (Q not empty) u = ExtractMin(Q); for each v  Adj[ u ] if (v  Q and w( u,v ) < key[ v ]) p[v] = u; key[v] = w(u,v);

14 10

3

6 4 5

2

9

15

8

Red vertices have been removed from Q

u

Docsity.com

Prim’s Algorithm

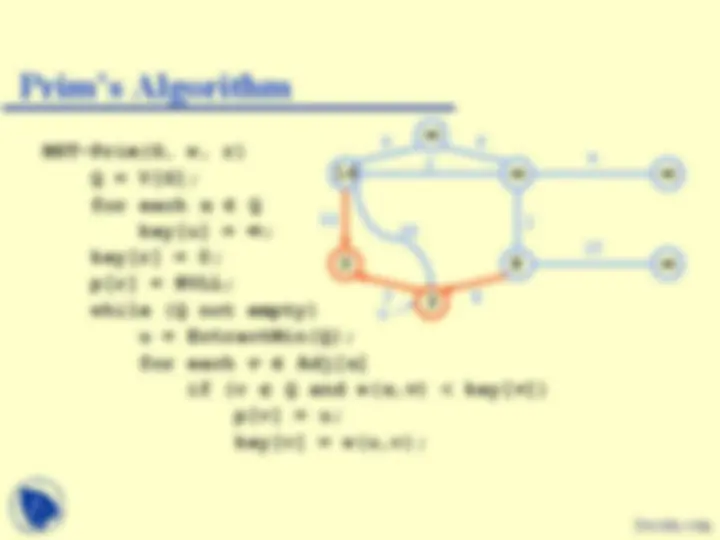
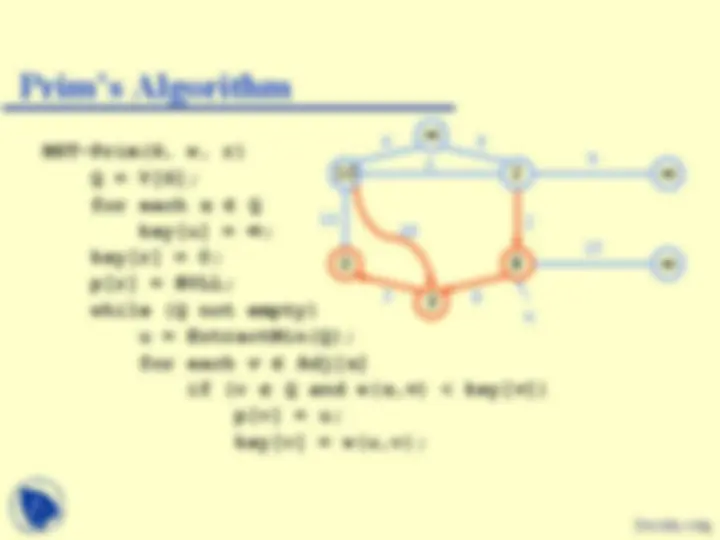
MST-Prim(G, w, r) Q = V[G]; for each u  Q key[u] = ; key[r] = 0; p[r] = NULL; while (Q not empty) u = ExtractMin(Q); for each v  Adj[ u ] if (v  Q and w( u,v ) < key[ v ]) p[v] = u; key[v] = w(u,v);

14 10

3

6 4 5

2

9

15

8

u

Docsity.com

Prim’s Algorithm

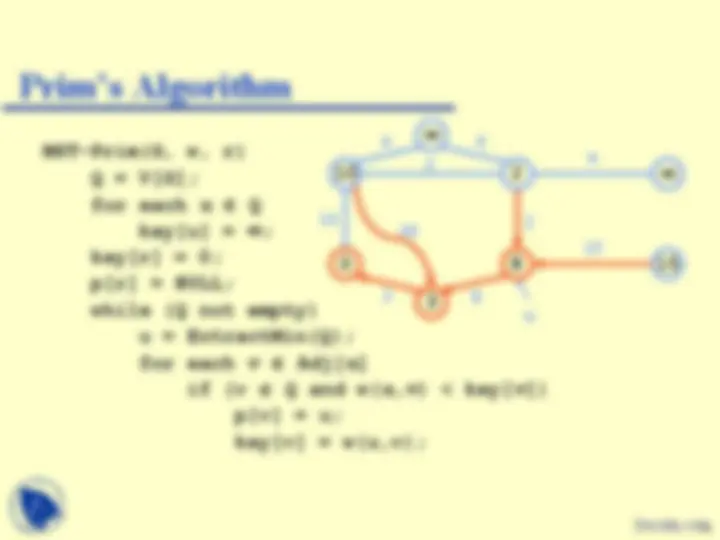
MST-Prim(G, w, r) Q = V[G]; for each u  Q key[u] = ; key[r] = 0; p[r] = NULL; while (Q not empty) u = ExtractMin(Q); for each v  Adj[ u ] if (v  Q and w( u,v ) < key[ v ]) p[v] = u; key[v] = w(u,v);

14 10

3

6 4 5

2

9

15

8 u

Docsity.com