Merge Sort, Quick Sort-Algorithm Design and Analysis for Sorting-Lecture Slides, Slides of Design and Analysis of Algorithms

Download Merge Sort, Quick Sort-Algorithm Design and Analysis for Sorting-Lecture Slides and more Slides Design and Analysis of Algorithms in PDF only on Docsity!

Sorting Algorithms

Merge Sort

Quick Sort

2

Overview

 Divide and Conquer

 Merge Sort

 Quick Sort

4

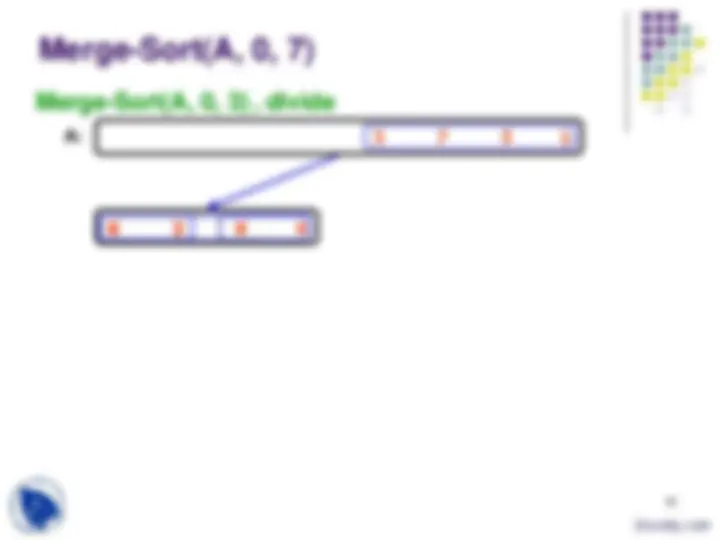
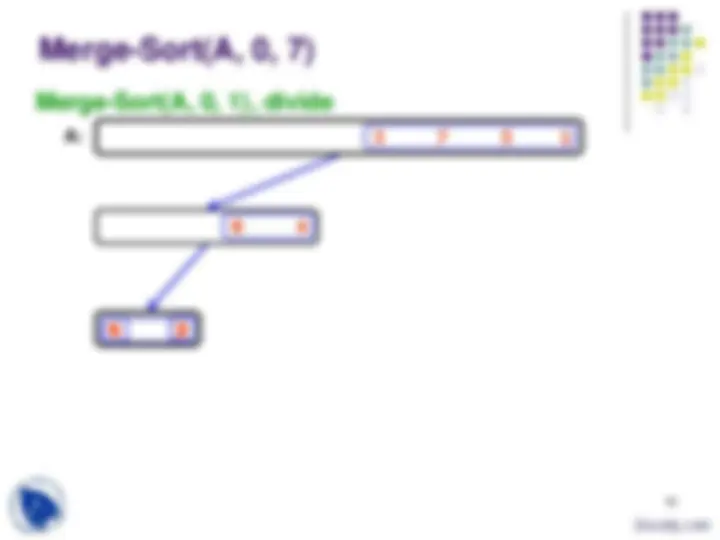
Divide and Conquer - Sort

Problem:

 Input: A[left..right] – unsorted array of integers

 Output: A[left..right] – sorted in non-decreasing

order

5

Divide and Conquer - Sort

1. Base case

at most one element (left ≥ right), return

2. Divide A into two subarrays: FirstPart, SecondPart

Two Subproblems:

sort the FirstPart sort the SecondPart

3. Recursively

sort FirstPart sort SecondPart

4. Combine sorted FirstPart and sorted SecondPart

7

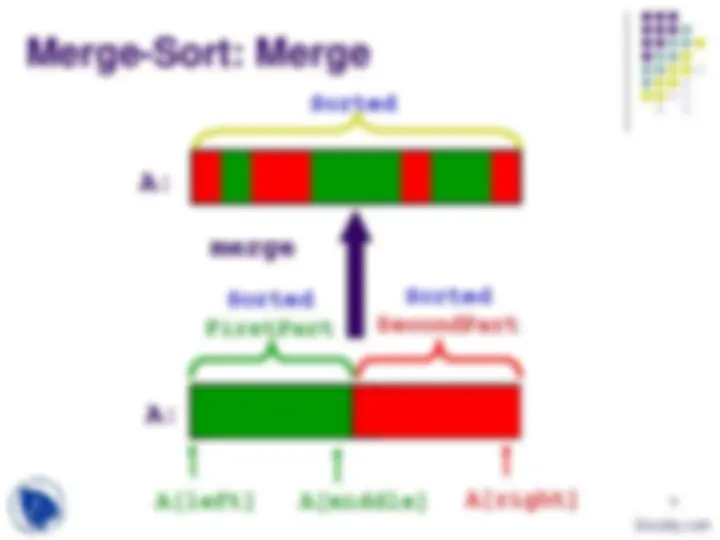
Merge Sort: Idea

Merge

Recursively sort

Divide into two halves

FirstPart (^) SecondPart

FirstPart SecondPart

A

A is sorted!

8

Merge Sort: Algorithm

Merge-Sort (A, left, right)

if left ≥ right return

else

middle ← b(left+right)/2

Merge-Sort (A, left, middle)

Merge-Sort (A, middle+1, right)

Merge (A, left, middle, right)

Recursive Call

10

L: R:

Temporary Arrays

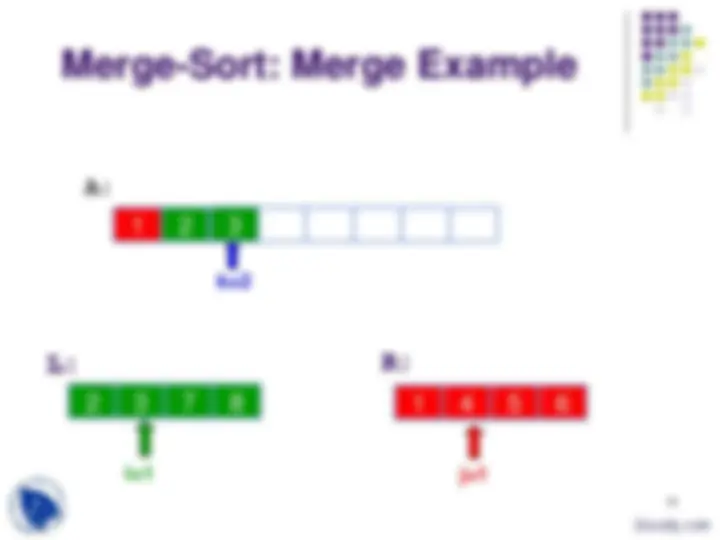
Merge-Sort: Merge Example

A: 2 3 7 8 1 4 5 6

11

Merge-Sort: Merge Example

L:

A:

R:

i=0 (^) j=

k=

13

Merge-Sort: Merge Example

L:

A:

R:

i=

k=

j=

14

Merge-Sort: Merge Example

L:

A:

R:

i=2 j=

k=

16

Merge-Sort: Merge Example

L:

A:

R:

i=2 (^) j=

k=

17

Merge-Sort: Merge Example

L:

A:

R:

k=

i=2 (^) j=

19

Merge-Sort: Merge Example

L:

A:

R:

i=4 j=

k=

20

Merge(A, left, middle, right)

**1. n 1 ← middle – left + 1

2. n 2 ← right – middle
3. create array L[n 1 ], R[n 2 ]
4. for i ← 0 to n 1 - 1 do L[i] ← A[left +i]
5. for j ← 0 to n 2 - 1 do R[j] ← A[middle+j]
6. k ← i ← j ← 0
7. while i < n 1 & j < n 2
8. if L[i] < R[j]
9. A[k++] ← L[i++]
10. else
11. A[k++] ← R[j++]
12. while i < n 1
13. A[k++] ← L[i++]
14. while j < n 2
15. A[k++] ← R[j++]** (^) n = n 1 +n 2

Space: n Time : cn for some constant c