Assignment Model: Minimizing Distance Traveled by Officials in Basketball Games, Lecture notes of Management Theory

Download Assignment Model: Minimizing Distance Traveled by Officials in Basketball Games and more Lecture notes Management Theory in PDF only on Docsity!

Solution of the

Assignment

Model

Assignment model

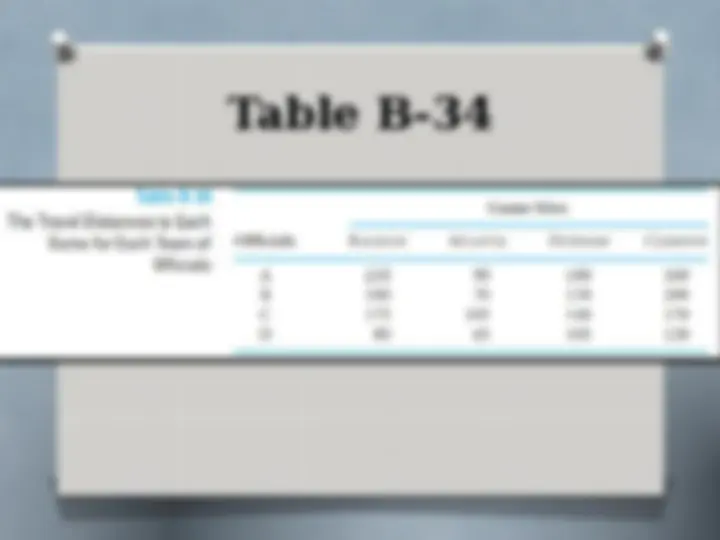
The assignment model is a special form of a linear programming model that is similar to the transportation model. There are differences, however. In the assignment model, the supply at each source and the demand at each destination are limited to one unit each.

The supply is always one team of officials, and the demand is for only one team of officials at each game. Table B-34 is already in the proper form for the assignment. The first step in the assignment method of solution is to develop an opportunity cost table. We accomplish this by first subtracting the minimum value in each row from every value in the row. These computations are referred to as row reductions. We applied a similar principle in the VAM method when we determined penalty costs. In other words, the best course of action is determined for each row, and the penalty or “lost opportunity” is developed for all other row values. The row reductions for this example are shown in Table B-35.

Next, the minimum value in each column is subtracted from all column values. These computations are called column reductions and are shown in Table B-36, which represents the completed opportunity cost table for our example. Assignments can be made in this table wherever a zero is present. For example, team A can be assigned to Atlanta. An optimal solution results when each of the four teams can be uniquely assigned to a different game.

A test to determine whether four unique assignments exist in Table B- is to draw the minimum number of horizontal or vertical lines necessary to cross out all zeros through the rows and columns of the table. For example, Table B- shows that three lines are required to cross out all zeros.

No matter how the lines are drawn in Table B-38, at least four are required to cross out all the zeros. This indicates that four unique assignments can be made and that an optimal solution has been reached. Now let us make the assignments from Table B-38.

These assignments and their respective distances (from Table B-

34. are summarized as follows:

Now let us go back and make the initial assignment of team A to Clemson (the alternative assignment we did not initially make). This will result in the following set of assignments:

• Table B-
• Table B-
• Table B-
• Table B-
• Table B-
• Table B-

In solving this model, one team of officials would be assigned to the dummy column. If there were five games and only four teams of officials, a dummy row would be added instead of a dummy column. The addition of a dummy row or column does not affect the solution method.