Download Linear Homogenous Recurrence - Discrete Mathematics - Solved Homework and more Slides Discrete Mathematics in PDF only on Docsity!
CS173: Discrete Mathematical Structures
Spring 2006
Homework
Due 04/16/06, 8am
Solutions (78 points)
Linear Homogenous Recurrence with Constant Coefficients
- (27 points)
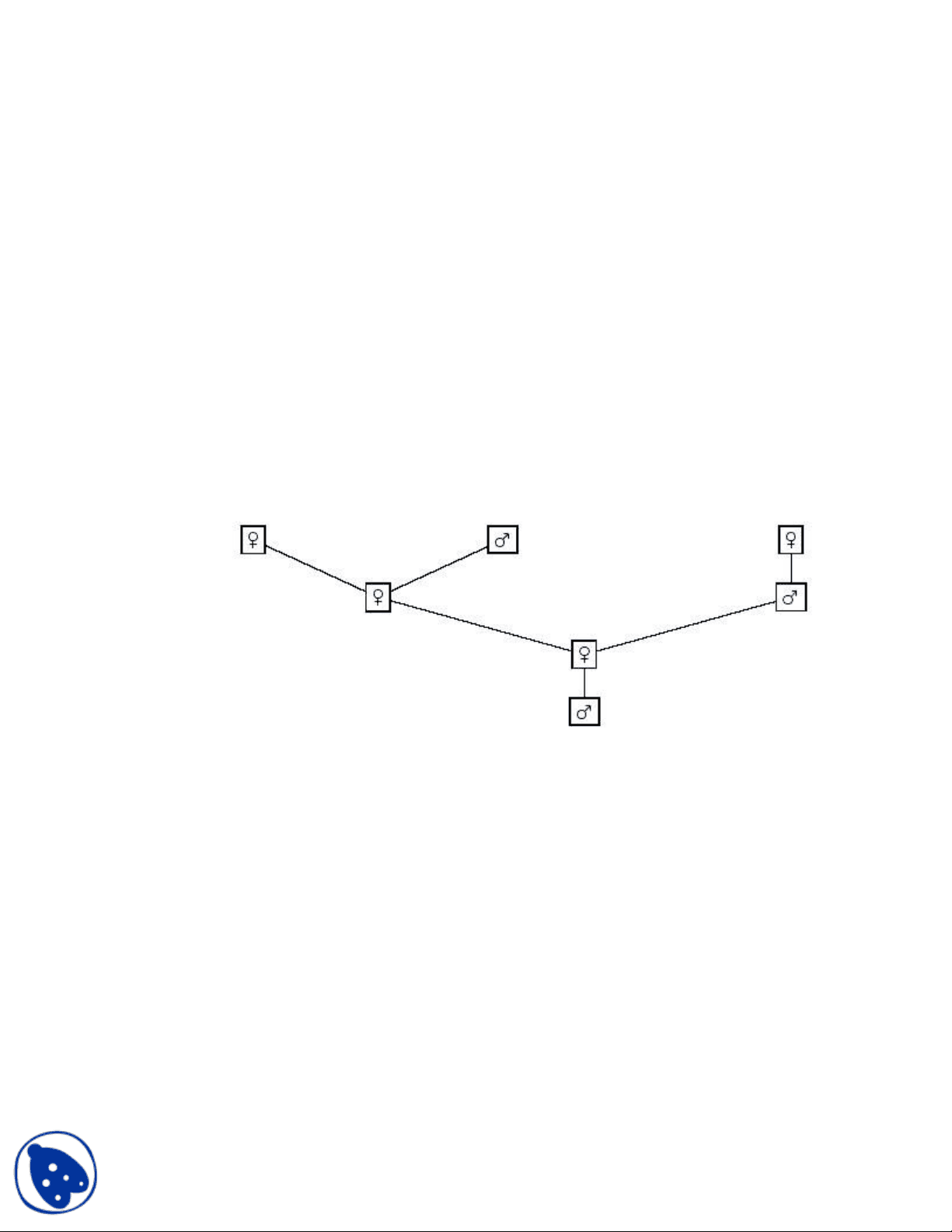
Consider the reproductive cycle of bees. Each male bee has a mother but no father. Each female bee has both a mother and a father. a. Draw a family tree of 4 generations for a male bee. (The male bee, his parent, his grandparents, and his great-grandparents are included in the tree.)
Solution (3 pts):
b. How many ancestors does a male bee have in generation 1 (his parent), generation 2 (his grandparents), and generation 3 (his great-grandparents) respectively? Find a relation between these three numbers.
Solution (2 pts): 1, 2, and 3. 3 = 1 + 2.
c. Find a general recurrence relation for the number of ancestors a male bee has in generation n. What are its initial conditions (You may want to start n from 1)?
Solution (5 pts, 3 pts for the recurrence and 1 for each initial condition): G n ( ) = G n( −1) + G n( −2) G(1) = 1 , G(2) = 2. d. Now we are gonna solve this recurrence. You may want to follow these steps:
i. Rewrite your recurrence so that the right side of the equation is zero. Solution (1 pt): G(n) – G(n-1) – G(n-2) = 0
ii. What is its characteristic equation? Solution (1 pt): r 2 − r− 1 = 0
iii. Find roots for the characteristic equation.
Solution (2 pts): (^1 )
r r
iv. Write down its general solution.
Solution (2 pts):
G n = A +^ n^ +B − n
v. The general solution has unknown coefficients. Apply the initial conditions of the recurrence and find an equation system in these unknown coefficients. Solve these coefficients. Solution (2 pts):
(1) (^1 5 )^1 (^1 5 )^1 2 2
G A B
(2) (^1 5 ) 2 (^1 5 )^2
G A B
A B A
A B B
+^ =^ =
+^ −^ −
+^ =^ =
vi. Finally, what does your unique solution of the recurrence look like? ☺ Solution (2 pts): 5 5 1 5 5 5 1 5 ( ) ( ) ( ) 10 2 10 2
G n = +^ +^ n^ + −^ − n
e. What famous recurrence are you actually solving? Solution (1 pt): This is just Fibonacci sequence. Note that coefficients vary according to different initial conditions.
f. Prove your solution using mathematical induction!
Solution (6 pts: 1 for base case, 2 pts for IH, and 3 pts for inductive step):
Base case: check G(1) and G(2). True. Inductive Hypothesis: Assume that
- (2 pts) solve for A and B: (^1)
A B A
A B B
+^ =^ = −
+^ ⋅^ =^ =
- (2 pts) unique solution: a n = − + 1 2 4⋅ n Finally, plugging this to the equation an − bn = 2 an (^) − 1 , we get b n = 1 + 4 n. (3 pts)
Linear NONhomogenous Recurrence with Constant Coefficients
- (31 points)
Suppose there are two goats on an island initially. The number of goats on the island doubles very year by natural reproduction, and some goats are either added or removed each year.
a. Construct a recurrence relation for the number of goats on the island at the start of the nth year, assuming that during each year an extra 100 goats are put on the island. Solution: (3 points, 1 for initial condition and 2 for the formula) Let an represent the number of goats on the island at the start of the nth year. The initial condition is a 1 = 2. The relation is: an = 2 an (^) − 1 + 100
b. Solve the recurrence relation from part (a) to find the number of goats on the island at the start of the nth year. Solution: (10 pts) The associated homogenous recurrence relation is an = 2 an (^) − 1
The solution is a n= α 2 n(2 pts).
The particular solution is a polynomial of degree 0, namely a constant, an = c(2 pts). Plugging this into the recurrence relation gives c = 2c+100. Therefore, c = -100. The particular solution is an = − 100 and the general solution
is an= α 2 n− 100 (3 pts).
Plugging in the initial condition and solving for α gives
us 2 = 2 α− 100 and α = 51. Therefore, the formula is
an = 51 2⋅ n− 100 (3 pts)
c. Construct a recurrence relation for the number of goats on the island at the start of the nth year, assuming that n goats are removed during the nth year from each n ≥ 3 and i. The removal occurs after the natural reproduction. ii. The removal occurs before the natural reproduction. Solution: (8 pts: 3 pts for each, and 2 for initial conditions)
(i) an = 2 an (^) − 1 −n (ii) an = 2( an (^) − 1 − n) = 2 an (^) − 1 − 2 n For both problems, the initial conditions are a 1 = 2, a 2 = 4. There are no goats being removed during first two years.
d. Solve the recurrence relation from part (c) subpart (i) to find the number of goats on the island at the start of the nth year Solution: (10 pts, same as part (b)) The associated homogenous recurrence relation is an = 2 an (^) − 1
The solution is a n= α 2 n The particular solution is a polynomial of degree
1, say, an = cn + d. Plugging this into the recurrence relation gives ( −c + 1) n + (2 c − d) = 0. Therefore, c = 1 and d = 2. The particular solution
is an = n+ 2 and the general solution is an = α 2 n+ n+ 2. Plugging in the
initial condition and solving for α gives us 4 = 4 α + 4 so α = 0. Therefore,
the formula is an = n+ 2 For all n ≥ 2 and a 1 = 2.
