Lecture Notes for CSC: Principles of Programming Languages, Lecture notes of Programming Languages

Download Lecture Notes for CSC: Principles of Programming Languages and more Lecture notes Programming Languages in PDF only on Docsity!

David Liu

Principles of Programming

Languages

Lecture Notes for CSC 324 (Version 2. 1 )

Department of Computer Science

University of Toronto

Contents

Prelude: The Study of Programming Languages

It seems to me that there have been two really clean, consistent models of programming so far: the C model and the Lisp model. These two seem points of high ground, with swampy lowlands between them. Paul Graham

As this is a “programming languages” course, you might be wondering: are we going to study new programming languages, much in the way that we studied Python in CSC 108 or even Java in CSC 207? Yes and no.

You will be introduced to new programming languages in this course; most notably, Racket and Haskell. However, unlike more introductory courses like CSC 108 and CSC 207 , in this course we leave learning the basics of these new languages up to you. How do variable assignments work? What is the function that finds the leftmost occurrence of an element in a list? Why is this a syntax error? These are the types of questions that we expect you to be able to research and solve on your own.^1 Instead, we focus on the ways in which these languages (^1) Of course, we’ll provide useful tu- torials and links to standard library references to help you along, but it will be up to you to use them.

allow us to express ourselves; that is, we’ll focus on particular affordances of these languages, considering the design and implementation choices the creators of these languages made, and compare these decisions to more familiar languages you have used to this point.

Programs and programming languages

We start with a simple question: what is a program? We are used to thinking about programs in one of two ways: as an active entity on our computer that does something when run; or as the source code itself, which tells the computer what to do. As we develop more and more sophisticated programs for more targeted domains, we often lose sight of one crucial fact: that code is not itself the goal, but instead a means of communication to the computer describing what we want to achieve.

A programming language, then, isn’t just the means of writing code, but a true language in the common sense of the word. Unlike what linguists call natu-

8 david liu

ral languages, which often carry ambiguity, nuance, and errors, programming languages target machines, and so must be precise, unambiguous, and perfectly understandable by mechanical algorithms alone. This makes the rules governing programming languages quite inflexible, which is often a source of trouble from beginners. Yet once mastered, the clarity afforded by these languages enables humans to harness the awesome computational power of modern technology. But even this lens of programming languages as communication is incomplete. Unlike natural languages, which have evolved over millennia, often organically without much deliberate thought,^2 programming languages are not even a cen- (^2) This is not to minimize the work of language deliberative bodies like the Oxford English Dictionary, but to point out that language evolves far beyond what may be prescribed.

tury old, and were explicitly designed by humans. As programmers, we tend to lose sight of this, taking our programming language for granted—quirks and oddities and all. But programming languages exhibit the same fascinating de- sign questions, trade-offs, and limitations that are inherent in all software design. Indeed, the various software used to implement programming languages—that is, to take human-readable source code and enable a computer to understand it—are some of the most complex and sophisticated programs in existence to- day.

The goal of this course, then, is to stop taking programming languages for granted; to go deeper, from users of programming languages to understanding the design and implementation of these languages.

Syntax and grammars

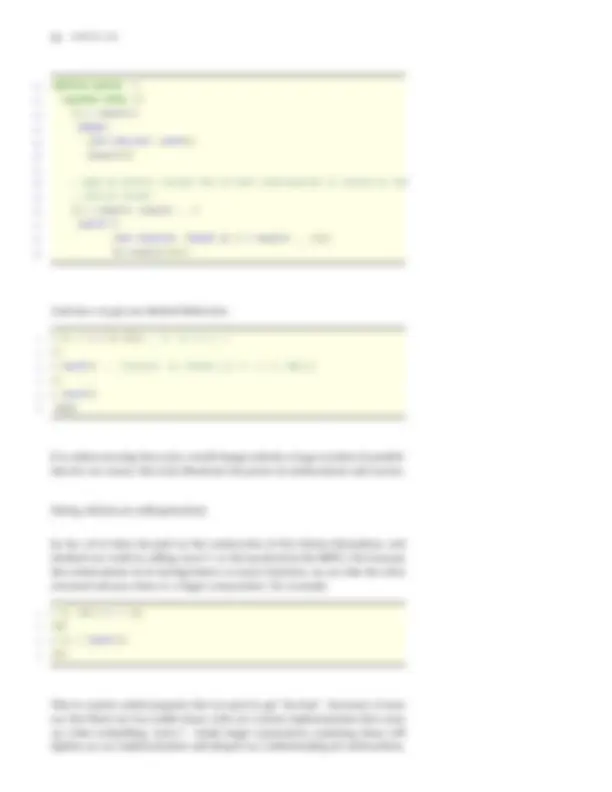
The syntax of a programming language is the set of rules governing what the allowed expressions of a programming language can look like; these are the rules governing allowed program structure. The most common way of specifying the syntax of a language is through a grammar, which is a formal description of how to generate expressions by substitution. For example, the following is a simple grammar to generate arithmetic expressions:

1 = NUMBER 2 | '(' ')' 3 4 = '+' | '-' | '*' | '/'

We say that the left-hand side names and are non-terminal symbols, meaning that we generate valid expressions by substituting for them using these grammar rules. By convention, we’ll put angle brackets around all non-terminal symbols.

The all-caps NUMBER is a terminal symbol, representing any numeric literal (e.g., 3 or -1.5).^3 The vertical bar | indicates alternatives (read it as “or”): for example, (^3) We’ll typically use INTEGER when we need to instead specify any integral literal.

can be replaced by any one of the strings '+', '-', '*', or '/'.

It is important to note that this grammar is recursive, as an can be re- placed by more occurrences of . This should match your intuition about

10 david liu

4. AST node types are often in rough correspondence to the grammar rules of a language.^5 So for example, the language’s syntax could contain a grammar (^5) Note that this is not necessarily exact; we are skipping over details of parsing and basic syntax analysis that many compilers often do before producing an AST.

rule for what a function definition looks like:

1 <function-def> = 'def' '(' [ ','] ... ')' ':' ' \n '

And when parsed, a program’s AST might include a “function definition” node with children for the name, parameters, and body of the function.

As we’ll start to see in the next chapter, abstract syntax trees enable us to avoid the idiosyncracies of program syntax and instead get to interesting operations on programs themselves.

Semantics and evaluation

You may have noticed in the previous section that we used the term expression to describe the inputs of our parsing. This may strike you as a little strange, since the term program usually connotes much more than this. Most modern program- ming languages, including Python, Java, and C, are fundamentally imperative in nature: inspired by the Turing machine model of computation, programs in these languages are organized around statements corresponding to instructions that the computer should execute.^6 In this model, we think of “running” a pro- (^6) “Statement” here includes larger gram as telling the computer to execute the instructions found in our program; syntactic “block” structures like loops. the result of running the program is whatever happens when these instructions are executed.

While it is certainly a familiar model of computation, and tracks closely to what computer hardware actually requires, one of the downsides of this model is its inherent complexity. In order to understand what a program means, we need to understand what each kind of statement does, and how it impacts control flow and underlying memory. The semantics of a programming language are the rules governing the meaning of programs written in that language; for im- perative style programs, we need to describe the meaning not just of individual expressions like 3 + 5 , but also the meaning of return (interrupts control flow), for (iterates through a specified range), and other keywords.

To simplify matters, we’ll stick with the easier task of understanding expression- based programs, in which a program is just an expression. In this model, run- ning a program means telling the computer to evaluate the expression; the result of running the program is simply the value of the expression after it has been evaluated.^7 7 Of course, all imperative languages have a notion of “evaluating expres- sions”; it’s just that those languages include a bunch of other stuff as well.

So the semantics of an expression-based language govern what the value of such programs are. This might seem simple, but it’s worth spelling out explicitly, because there are actually multiple ways of studying such semantics.

The denotational semantics of a programming language specify the abstract value of a program, drawing on formal definitions (e.g., from mathematics). We

principles of programming languages 11

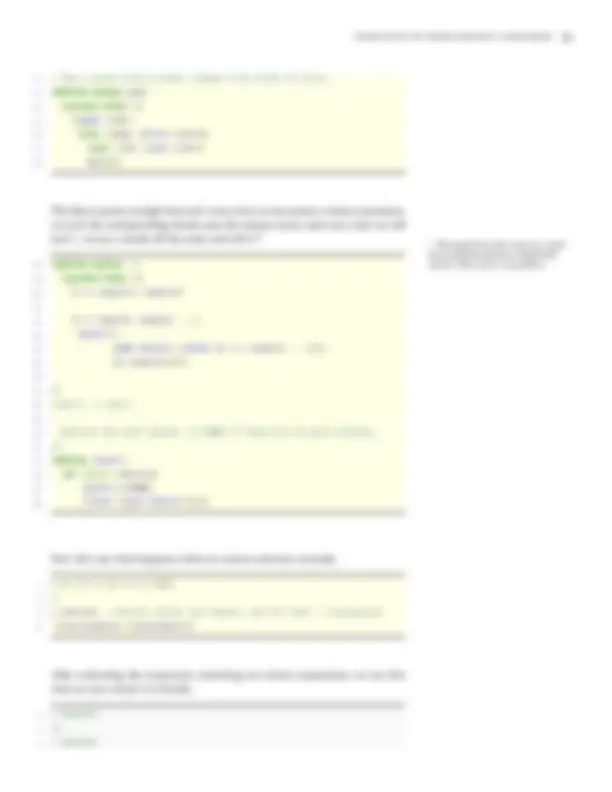
won’t go into the details here, but instead rely on your intuitions from math- ematics and basic programming. In the space below, we’ve listed several pro- grams (each consisting of just a single Python expression) that have the same denotational value 10 :

1 10 2 3 3 + 7 4 5 1 + (^3) ** 2 6 7 ord(' \n ') 8 9 ( lambda x: x + 3)(7) 10 11 list(range(50000000))[11]

That is, each of the above expressions, while written and parsed differently, produces the same result when evaluated; we would say that they have the same mathematical meaning, or the same value.

However, your gut probably tells you that this isn’t the full story. After all, even though these expressions might evaluate to the same value, how they each get to that value is quite different. The operational semantics of a programming language specify the evaluation steps used to determine the value of a program. In imperative-style languages, it is the operational semantics that are hardest to specify, as they deal with complexities of control flow, mutation, and func- tion calls. As we’ll see in the next chapter, specifying the operational semantics of expression evaluation alone—especially in a functional context—is generally straightforward.

While we will focus on denotational and operational semantics in this course, it is worth mentioning one other kind of semantics that comes up in programming languages. This is axiomatic semantics , where rather than focus on evaluation, we focus on what is true about each piece of a code segment. For example, we might argue that “this loop maintains the invariant that sum is the sum of the first i integers in list L”. Sound familiar? You used some of the axiomatic tools—invariants, variants, pre/postconditions—already in CSC 236!

Models of computation

It was in the 1930 s, years before the invention of the first electronic computing devices, that a young mathematician named Alan Turing created modern com- puter science as we know it. Incredibly, this came about almost by accident; he had been trying to solve a problem from mathematical logic: the Entschei- dungsproblem (“decision problem”), which asks whether an algorithm could de- cide if a logical statement is provable from a given set of axioms. Turing showed

principles of programming languages 13

1 def f(a): (^2 12) * a - 1 3 a 4 'hello' + 'goodbye'

Even though all three expressions in the body of f are evaluated each time the function is called, they are unable to influence the output of this function. We require sequences of statements (including keywords like return) to do anything useful at all! Even function calls, which might look like standalone expressions, are only useful if the bodies of those functions contain statements for the com- puter to execute.

In contrast to this instruction-based approach, Alonzo Church created a model called the lambda calculus in which expressions themselves are the fundamen- tal, and in fact only, unit of computation. Rather than a program being a se- quence of statements, in the lambda calculus a program is a single expression (possibly containing many subexpressions). And when we say that a computer runs a program, we do not mean that it performs operations corresponding to statements, but rather that it evaluates that single expression.

Two questions arise from this notion of computation: what do we really mean by the words “expression” and “evaluate”? Or in other words, what are the syntax and semantics of the lambda calculus? This is where Church borrowed func- tions from mathematics, and why the programming paradigm that this model spawned is called functional programming. In the lambda calculus, an expres- sion is one of three things:

1. An identifier (or variable ): a, x, yolo, etc.
2. A function expression : λ x.x, for example. This expression represents a func- tion that takes one parameter x, and returns it—in other words, this is the identity function.
3. A function application (or function call ): f expr. This expression applies the function f to the expression expr.

Now that we have defined our allowable expressions, what do we mean by evaluating them? To evaluate an expression means performing simplifications to it until it cannot be further simplified; we’ll call the resulting fully-simplified expression the value of the expression.

This definition meshes well with our intuitive notion of evaluation, but we’ve really just shifted the question: what do we mean by “simplifications?” In fact, in the lambda calculus, identifiers and function expressions have no simplification rules: in other words, they are themselves values, and are fully simplified. On the other hand, function application expression can be simplified, using the idea of substitution from mathematics. For example, suppose we apply the identity function to the variable hi: ( λ x.x) hi

14 david liu

We evaluate this by substituting hi for x in the body of the function, obtaining hi as a result.

Pretty simple, eh? As surprising as this may be, function-application-as-substitution is the only simplification rule for the lambda calculus! So if you can answer questions like “If f (x) = x^2 , then what is f ( 5 )?” then you’ll have no trouble understanding the lambda calculus.

The main takeaway from this model is that function application (via substitu- tion) is the only mechanism we have to induce computation; functions can be created using λ and applied to values and even other functions, and through combining functions we create complex computations. A point we’ll return to again and again in this course is that functions in the lambda calculus are far more restrictive than the functions we’re used to from previous programming experience. The only thing we can do in the lambda calculus when evaluating a function application is substitute the arguments into the function body, and then evaluate that body, producing a single value. These functions have no concept of time to require a certain sequence of instructions, nor is there any external or global state that can influence their behaviour.

At this point the lambda calculus may seem at best like a mathematical curiosity. What does it mean for everything to be a function? Certainly there are things we care about that aren’t functions, like numbers, strings, classes and every data structure you’ve studied up to this point—right? But because the Turing ma- chine and the lambda calculus are equivalent models of computation, anything you can do in one, you can also do in the other! So yes, we can use functions to represent numbers, strings, and data structures; we’ll see this only a little in this course, but rest assured that it can be done.^11 And though the Turing machine (^11) If you’d like to do some reading on is more widespread, the beating heart of the lambda calculus is still alive and this topic, look up Church encodings. well, and learning about it will make you a better computer scientist.

A paradigm shift in you

The influence of Church’s lambda calculus is most obvious today in the func- tional programming paradigm, a function-centric approach to programming that has heavily influenced languages such as Lisp (and its dialects), ML, Haskell, and F#. You may look at this list and think “I’m never going to use these in the real world,” but support for functional programming styles is being adopted in more “mainstream” languages, such as LINQ in C# and lambdas in Java 8. Other languages like Python and JavaScript have supported the functional pro- gramming paradigm since their inception.

The goal of this course is not to convert you into the Cult of FP, but to open your mind to different ways of solving problems. After all, the more tools you have at your disposal in “the real world,” the better you’ll be at picking the best one for the job.

Along the way, you will gain a greater understanding of different programming language properties, which will be useful to you whether you are exploring new

1 Functional Programming: Theory and Practice

Any sufficiently complicated C or Fortran program contains an ad hoc, informally-specified, bug-ridden, slow implementation of half of Common Lisp. Greenspun’s tenth rule of programming

In 1958 , John McCarthy created Lisp , a bare-bones programming language based on Church’s lambda calculus.^1 Since then, Lisp has spawned many dialects (^1) Lisp itself is still used to this day; in fact, it has the honour of being the second-oldest programming language still in use. The oldest? Fortran.

(languages based on Lisp with some deviations from its original specifications), among which are Common Lisp, Clojure (which compiles to the Java Virtual Ma- chine), and Racket (a language used actively in educational and programming language research contexts).

In 1987 , it was decided at the conference Functional Programming Languages and Computer Architecture^2 to form a committee to consolidate and standardize exist- (^2) Now part of this one: http://www. ing non-strict functional languages, and so Haskell was born (we’ll study what icfpconference.org/ the term “non-strict” means in this chapter). Though mainly still used in the aca- demic community for research, Haskell has become more widespread as func- tional programming has become, well, more mainstream. Like Lisp, Haskell is a functional programming language: its main mode of computation involves defining pure functions and combining them to produce complex computation. However, Haskell has many differences from the Lisp family, both immediately noticeable and profound.

Our goal in this chapter is to expose you to some of the central concepts in pro- gramming language theory, and functional programming in particular, without being constrained to one particular language. So in this chapter, we’ll draw on examples from three languages: Racket, Haskell, and Python. Our hope here is that by studying the similarities and differences between these languages, you’ll gain more insights into the deep concepts in this chapter than by studying any one of these languages alone.

principles of programming languages 19

1 ; Racket 2 ( lambda ( ...) )

1 -- Haskell 2 <param> ... ->

1 # Python 2 lambda ... :

In each of the above examples, each is called a parameter of the func- tion, and must be an identifier. The is an expression called the body of the function.

For programmers that have never seen anonymous functions before, such func- tions might seem strange: what’s the point of writing a function if you don’t have a name to refer to it? While we’ll see some motivating examples later in this chapter, for now we’ll leave you with a different question: does every expression you write have a name?

Function application

Calling functions in each of the three languages is straightforward, but note that both Racket and Haskell use an unfamiliar syntax.

First, in Python a function call looks like most languages you’ve probably worked with before:

1 (, ...)

In Racket, the function expression goes inside the parentheses:^5 5 This syntax is known as Polish prefix notation. 1 ( ...)

One thing that trips students up is that in Racket, every parenthesized expres- sion is treated as a function call, except for the ones starting with keywords like lambda. This is in stark contrast with most programming languages, in which ex- pressions are often enclosed in (redundant) parentheses to communicate group- ing explicitly. Racket doesn’t have the concept of “redundant” parentheses!

20 david liu

In Haskell, parentheses are not required at all; instead, any two expressions separated by a space are considered a function call:

1 ...

Operators are functions

Consider common binary arithmetic operations like addition and multiplication, which we normally think of as being written infix, i.e., between its two argument expressions: 3 + 4 or 1.5 (^) * 10.

Again in the theme of the centrality of functions to our programming, it’s im- portant to realize that in fact, these operators are just functions, at least from a mathematical point of view.^6 In fact, all three of Racket, Haskell, and Python (^6) Formally, we might write something like + : R × R → R to represent the + operation as taking two real numbers and outputting a real number.

treat them as functions!

In Racket, operators are just identifiers that refer to built-in functions, and are called the same way any other function would be called:

1 > (+ 10 20) 2 30 3 > (* 3 5) 4 15

In Python, operators are implemented under the hood by delegating to various “dunder methods” for built-in classes:

1 >>> 10 + 20 2 30 3 >>> int.add(10, 20) # Equivalent to 10 + 20 4 30

Haskell uses a similar approach. Every infix operator (e.g., +) is a function whose name is the same as the operator, but enclosed in parentheses (e.g., (+)):

1 > 10 + 20 2 30 3 > (+) 10 20 4 30

Again, pretty weird! If you’ve never thought about it before, this might seem overly complex. Racket actually has the cleanest model (no infix operators, uni- form prefix syntax for all functions), at the cost of being more unfamiliar; Python