lect09b-interconnects-topology-routing, Slides of Computer Networks

Download lect09b-interconnects-topology-routing and more Slides Computer Networks in PDF only on Docsity!

Interconnection Networks:

Topology and Routing

Natalie EnrightJerger

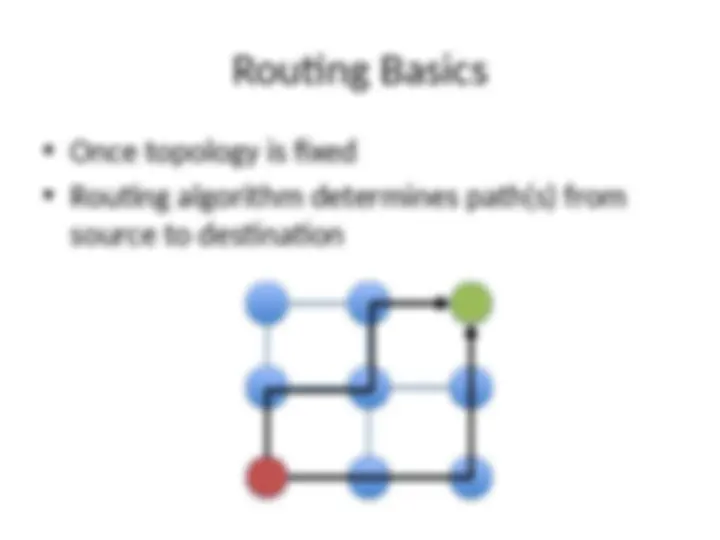
Topology Overview

Definition: determines arrangement of

channels and nodes in network

Analogous to road map

Often first step in network design

Routing and flow control build on properties

of topology

Latency

Time for packet to traverse network

• Start: head arrives at input port
• End: tail departs output port

Latency = Head latency + serialization latency

• Serialization latency: time for packet with Length L to

cross channel with bandwidth b (L/b)

Hop Count: the number of links traversed between

source and destination

• Proxy for network latency
• Per hop latency with zero load

Impact of Topology on Latency

Impacts average minimum hop count

Impact average distance between routers

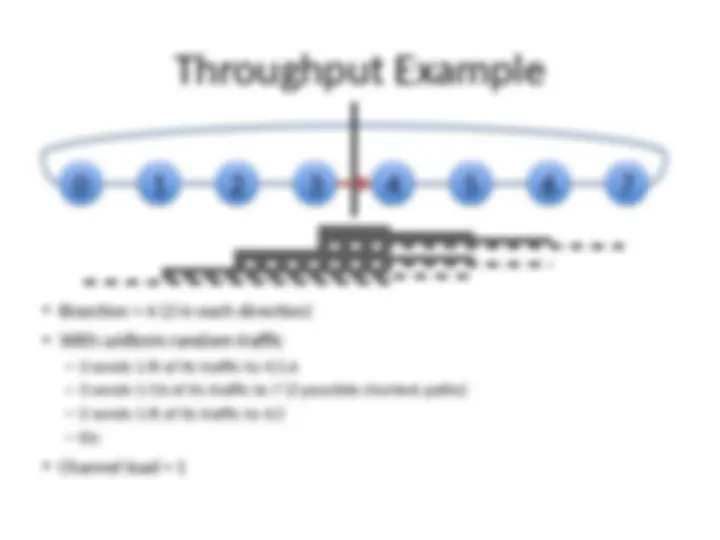
Bandwidth

Maximum channel load

Channel with largest fraction of traffic

Max throughput for network occurs when

channel saturates

Bottleneck channel

Bisection Bandwidth

Cuts partition all the nodes into two disjoint sets

• Bandwidth of a cut

Bisection

• A cut which divides all nodes into nearly half
• Channel bisection  min. channel count over all

bisections

• Bisection bandwidth min. bandwidth over all bisections

With uniform traffic

• ½ of traffic cross bisection

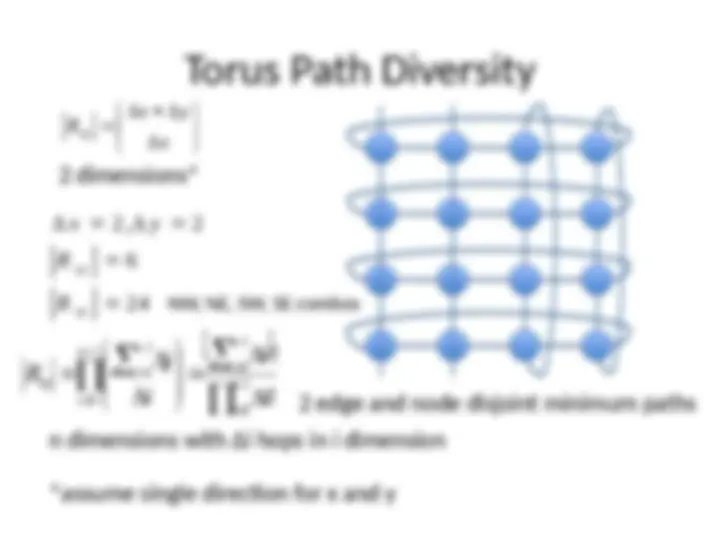
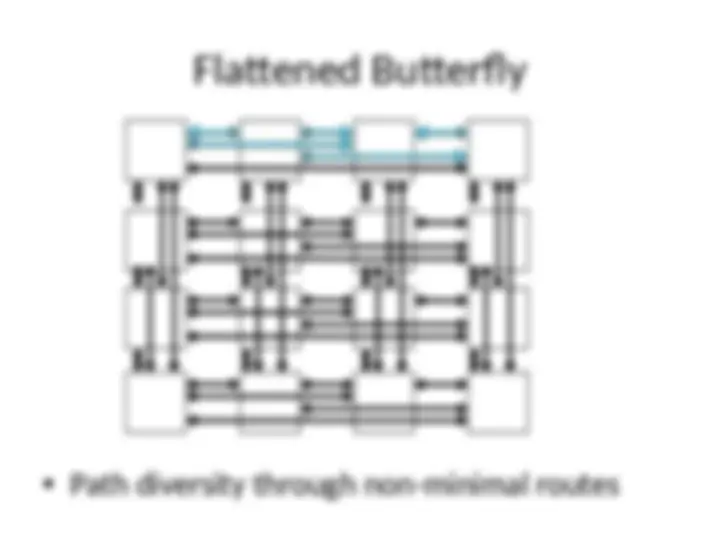
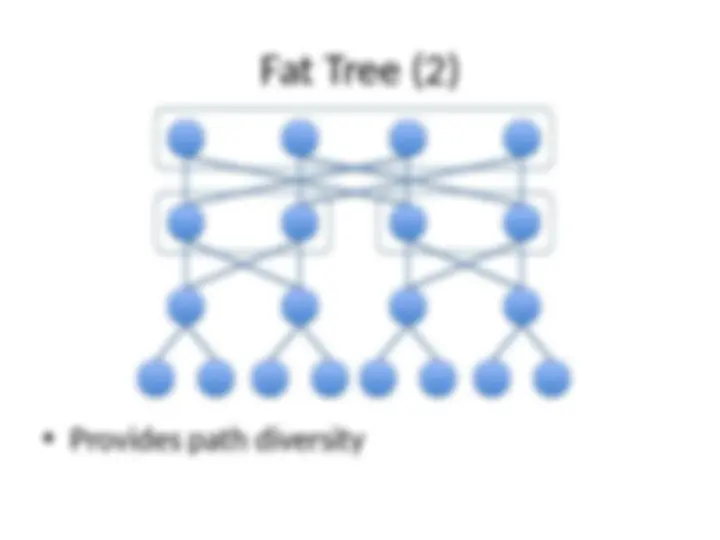
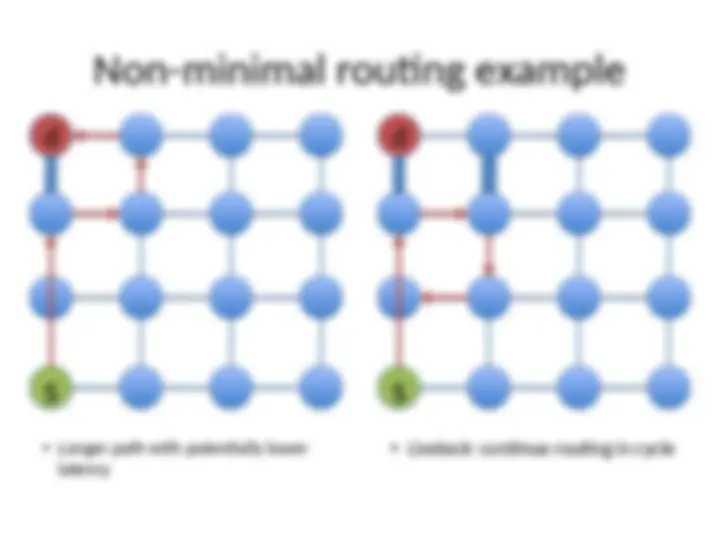
Path Diversity

Multiple minimum length paths between source

and destination pair

Fault tolerance

Better load balancing in network

Routing algorithm should be able to exploit path

diversity

We’ll see shortly

• Butterfly has no path diversity
• Torus can exploit path diversity

Path Diversity (2)

Edge disjoint paths: no links in common

Node disjoint paths: no nodes in common

except source and destination

If j = minimum number of edge/node disjoint

paths between any source-destination pair

Network can tolerate j link/node failures

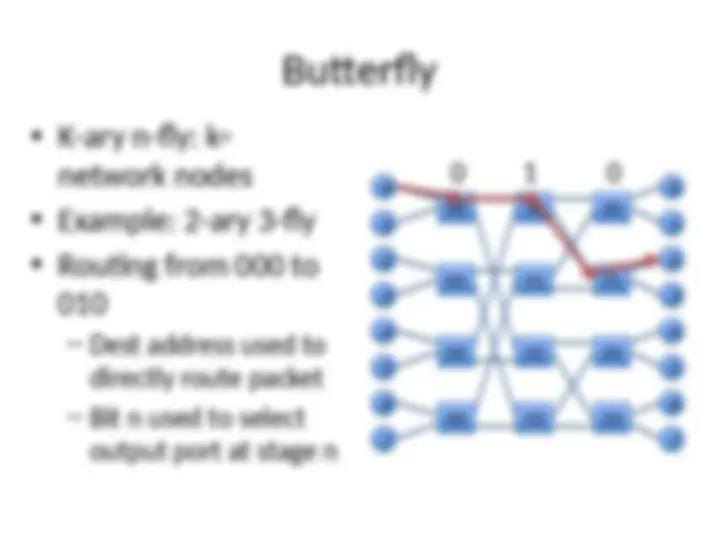
Direct & Indirect Networks

Direct: Every switch also network end point

Ex: Torus

Indirect: Not all switches are end points

Ex: Butterfly

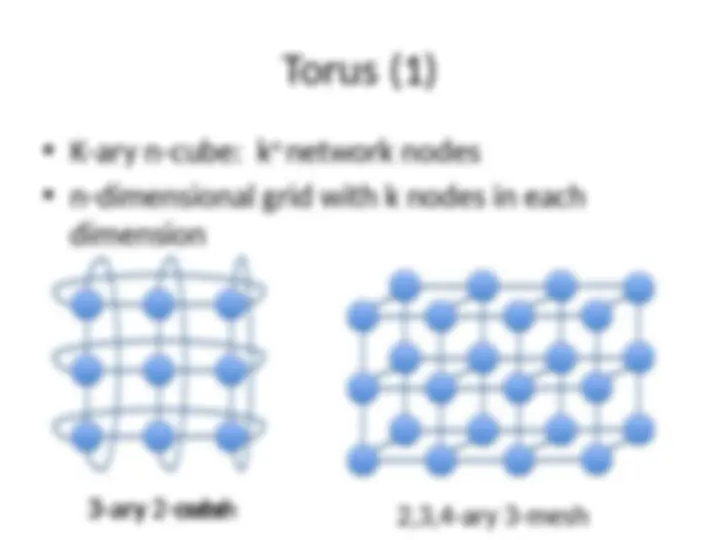
Torus (1)

K-ary n-cube: k

n

network nodes

n-dimensional grid with k nodes in each

dimension

3-ary 2-mesh 3-ary 2-cube

2,3,4-ary 3-mesh

Torus (3)

Hop Count:

Degree = 2n, 2 channels per dimension































k odd

k

k

n

k even

nk

H

4

1

4

4

min

Channel Load for Torus

Even number of k-ary (n-1)-cubes in outer

dimension

Dividing these k-ary (n-1)-cubes gives a 2 sets of

k

n-

bidirectional channels or 4k

n-

½ Traffic from each node cross bisection

k

N

N k

channel load   

Mesh has ½ the bisection bandwidth of torus

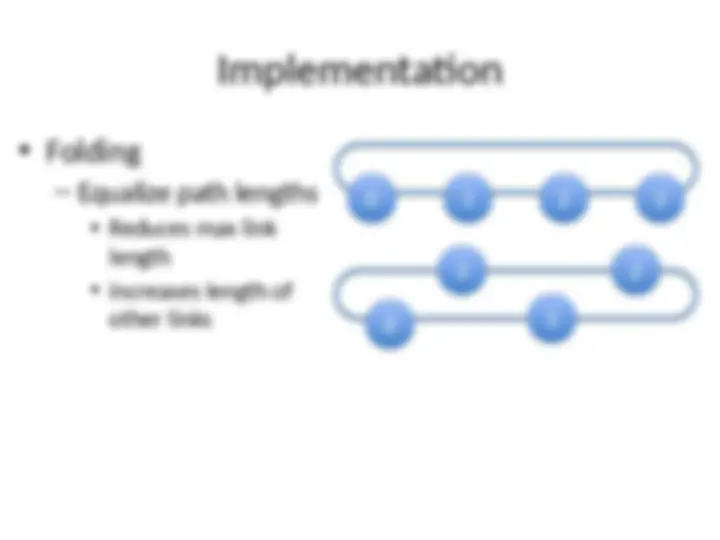
Implementation

Folding

Equalize path lengths

• Reduces max link

length

• Increases length of

other links

0

0 1

1 2

2 3

3

0

0

1

1

2

2 3

3

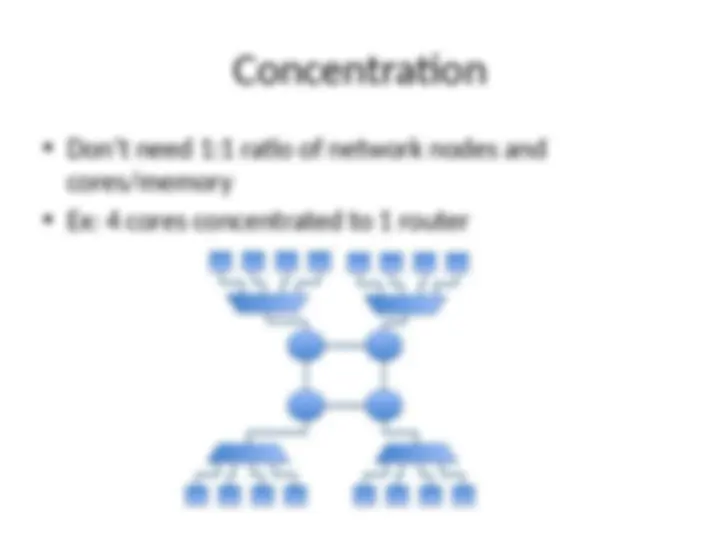
Concentration

Don’t need 1:1 ratio of network nodes and

cores/memory

Ex: 4 cores concentrated to 1 router