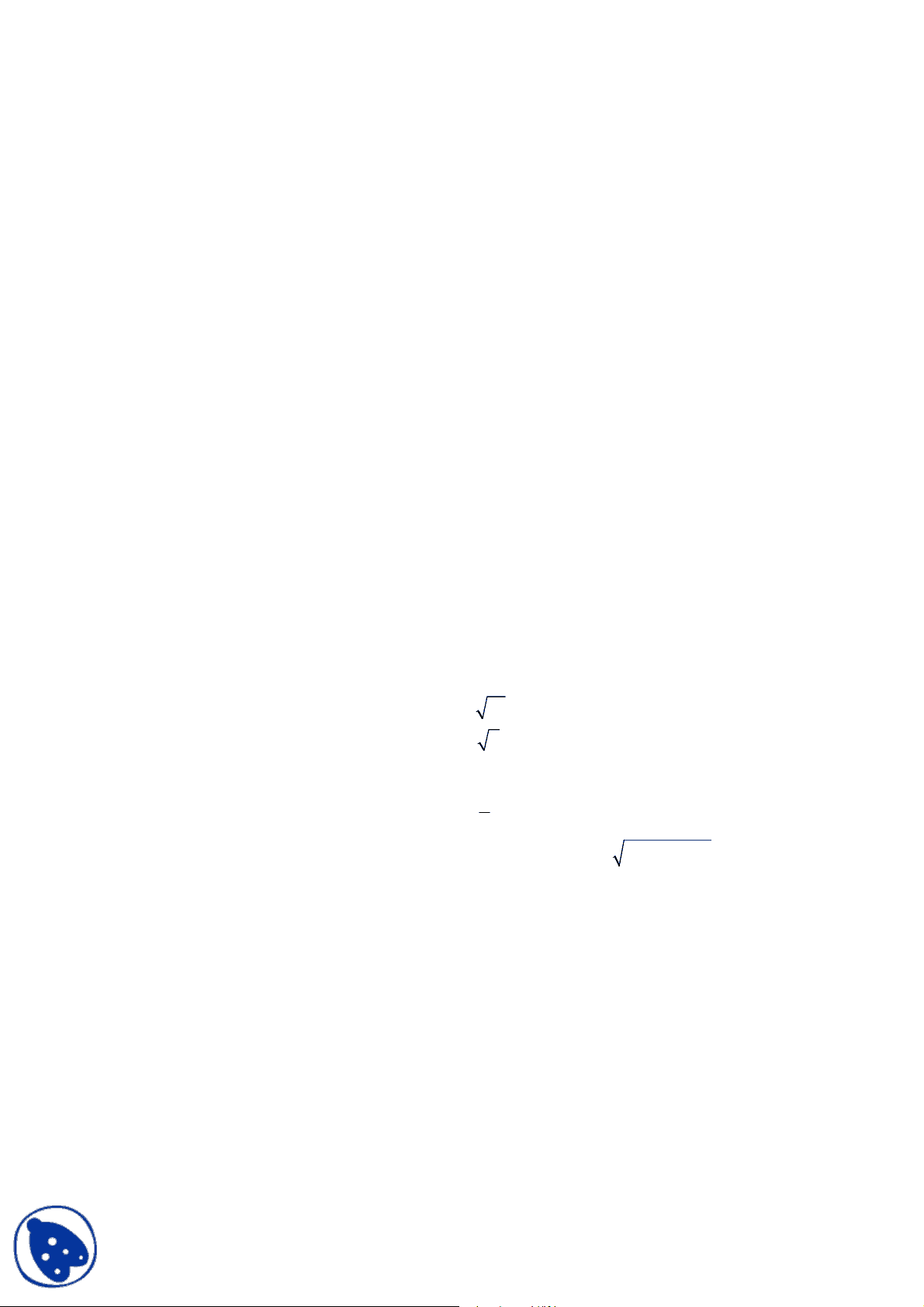



Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
During the study of discrete mathematics, I found this course very informative and applicable.The main points in these lecture slides are:Inverse Function, Define Function, Register Multiple Classes, Multiple Elements, Domain to Codomain, Graph of Original Function, Well-Defined Function, Non-Negative Value, Simple Translation, Indirect Proof
Typology: Slides
1 / 2

This page cannot be seen from the preview
Don't miss anything!
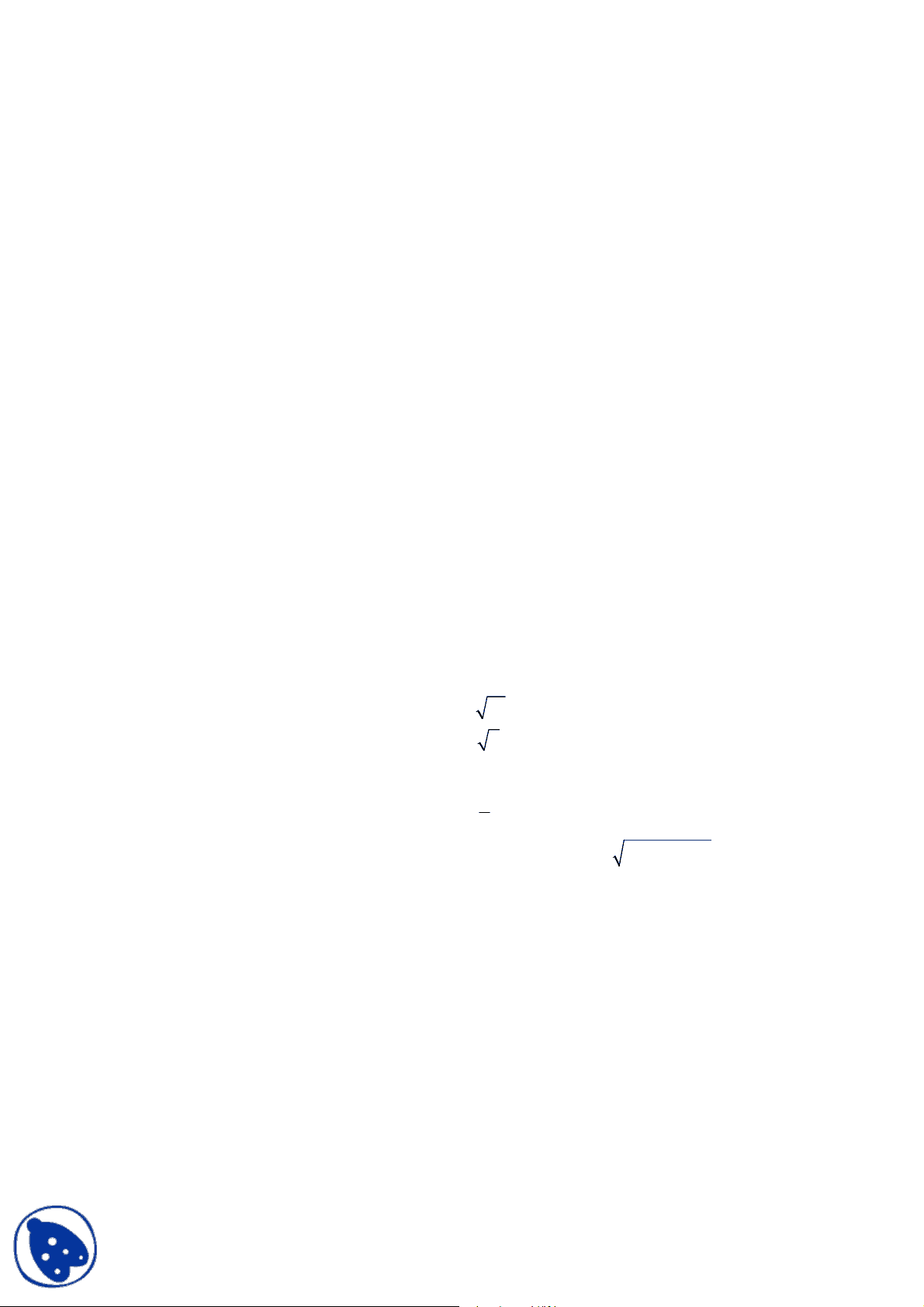

a) For x ∈ S and y ∈ C , we say y = f ( x ) if and only if student x has registered course y. Does f : S → C define a function? Why or why not? b) For x ∈ S and y ∈ PC ( PC is the power set of C ), we say y = f ( x ) if and only if student x has registered every course in set y. Does f : S → PC define a function? Why or why not? c) For x ∈ S and y ∈ PC ( PC is the power set of C ), we say y = f ( x ) if and only if student x has registered for every course in set y and for no course in set C − y. Does f : S → PC define a function? Why or why not?
a) f : Z → Z where f is defined by f ( x ) = x^2 b) f : Z → R where f is defined by f ( x ) = x c) f : R+^ → R+^ where f is defined by f ( x ) = log( x + 1) d) f : Z → N where f is defined by f ( x ) = x x e) f : R× R× R → R+^ ∪{0} where f is defined by f ( x , y , z ) = x^2 + y^2 + z^2 f) f : R× R → R× R where f is defined by f ( x , y ) = ( x + 1, y + 1)
Let f : S → T and g : T → U be functions. a) Prove that if g D f is one-to-one, so is f. b) Find an example where g D f is one-to-one but g is not one-to-one.
The Growth of Functions a) Show that x^3 is O ( x^4 ) but that x^4 is not O ( x^3 ). b) Give as good a big- O estimate as possible for each of the following (A formal proof is not required, but give your reasoning):
(^2) + n log 2 n^ +^1 3 n 3/ 2^ + 2 n + 4
2 n
c) Which of the functions in part b) above has the fastest growth rate?
d) Show that if f ( x ) is O (log b x ) where b > 1 , then f ( x ) is O (log a x ) where a > 1.