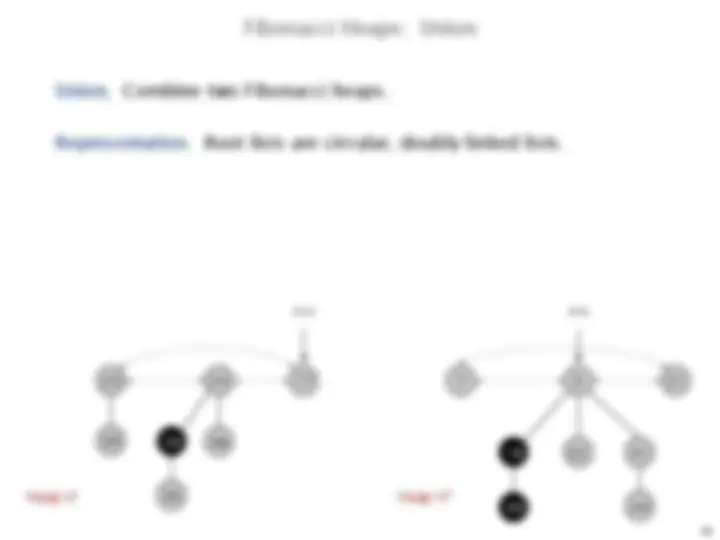
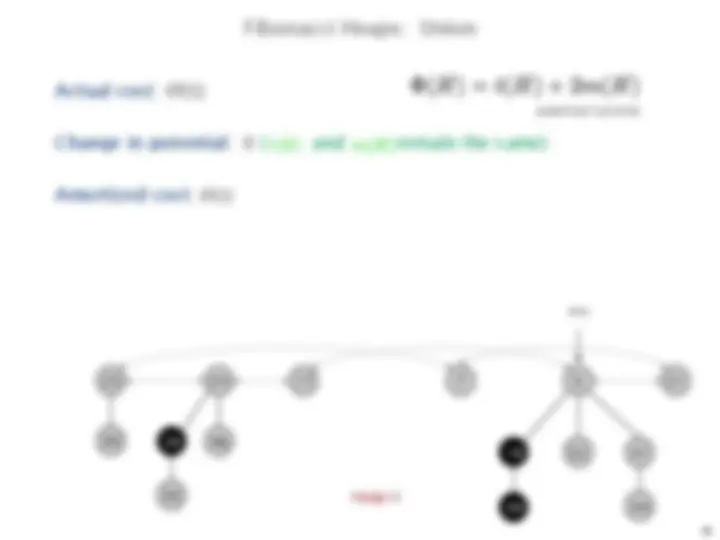
Download fibonacci heap in daa and more Essays (university) Design and Analysis of Algorithms in PDF only on Docsity!
COS 423 Theory of Algorithms • Kevin Wayne • Spring 2007
Adapted by Cheng Li and Virgil Pavlu
Fibonacci Heaps
Lecture slides adapted from:
- Chapter 20 of Introduction to Algorithms by Cormen, Leiserson, Rivest, and Stein.
- Chapter 9 of The Design and Analysis of Algorithms by Dexter Koze
Fibonacci Heaps
History. [Fredman and Tarjan, 1986]
Ingenious data structure and analysis.
Original motivation: improve Dijkstra's shortest path algorithm
(module 12) from to
Basic idea.
Similar to binomial heaps, but less rigid structure.
Binomial heap: eagerly consolidate trees after each insert.
Fibonacci heap: lazily defer consolidation until next extract-min.
V insert, V extract-min, E decrease-key
Fibonacci Heaps: Structure
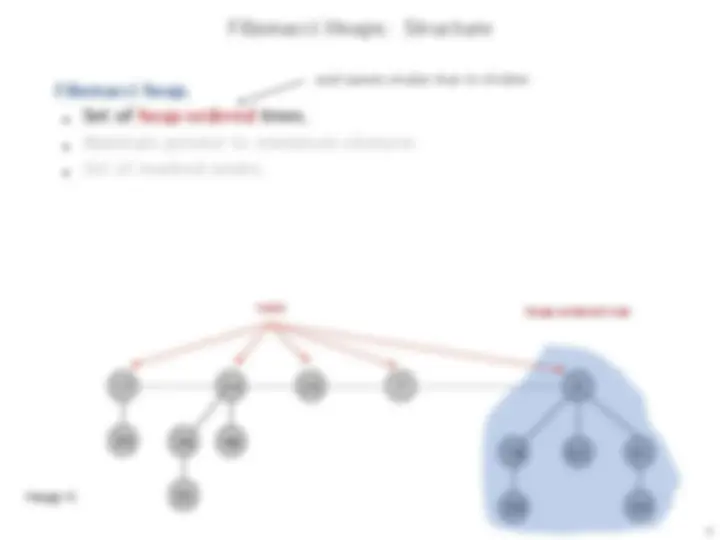
Fibonacci heap.
Set of heap-ordered trees.
Maintain pointer to minimum element.
Set of marked nodes.
Heap H
min
find-min takes O(1) time
Fibonacci Heaps: Structure
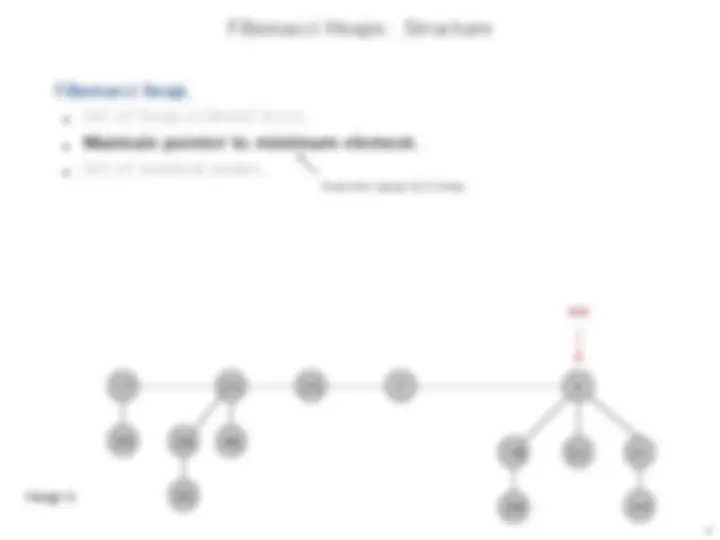
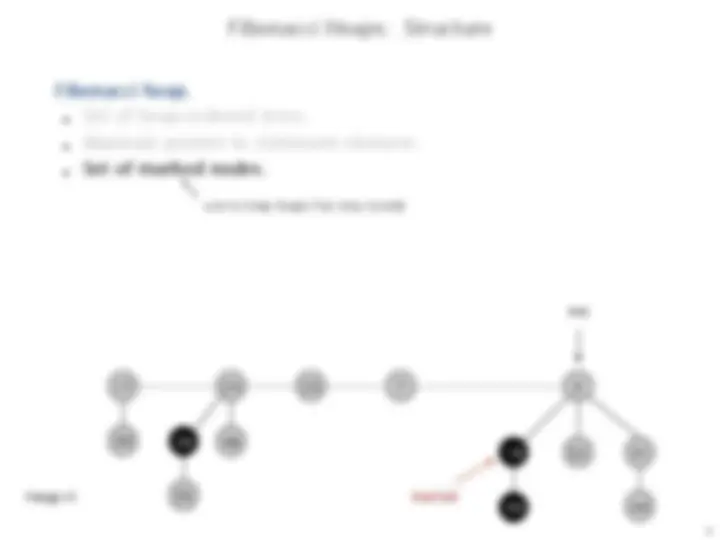
Fibonacci heap.
Set of heap-ordered trees.
Maintain pointer to minimum element.
Set of marked nodes.
Heap H
min
use to keep heaps flat (stay tuned)
marked
Fibonacci Heaps: Potential Function
Φ(H) = 5 + 2⋅3 = 11
min
Heap H
potential of heap H :
t(H) = 5 m(H) = 3
marked
This lecture is not a complete treatment of Fibonacci
heaps; in order to implement (code) and use them, more
details are necessary (see book). Our main purpose here is
to understand how the potential function works.
Next: analyze change in potential and amortized costs for
heaps operations:
- Insert (easy, required)
- Extract min (medium, required)
- Decrease Key (difficult, optional)
- Union (easy, required)
- Delete (medium, required)
Insert
Fibonacci Heaps: Insert
Insert.
Create a new singleton tree.
Add to root list; update min pointer (if necessary).
min
Heap H
insert 21
Fibonacci Heaps: Insert Analysis
Actual cost.
H’ = the heap after insert
Change in potential.
Amortized cost.
min
Heap H
potential of heap H
Linking Operation
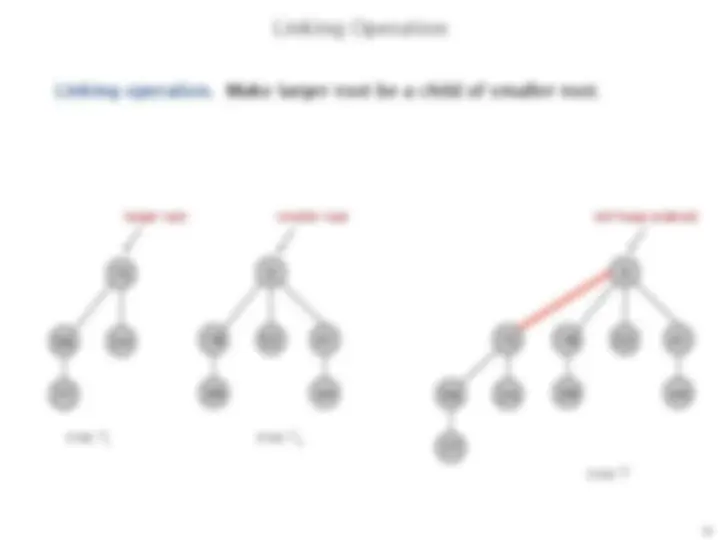
Linking operation. Make larger root be a child of smaller root.
tree T
1
tree T
2
tree T'
larger root smaller root still heap-ordered
Fibonacci Heaps: Extract-Min
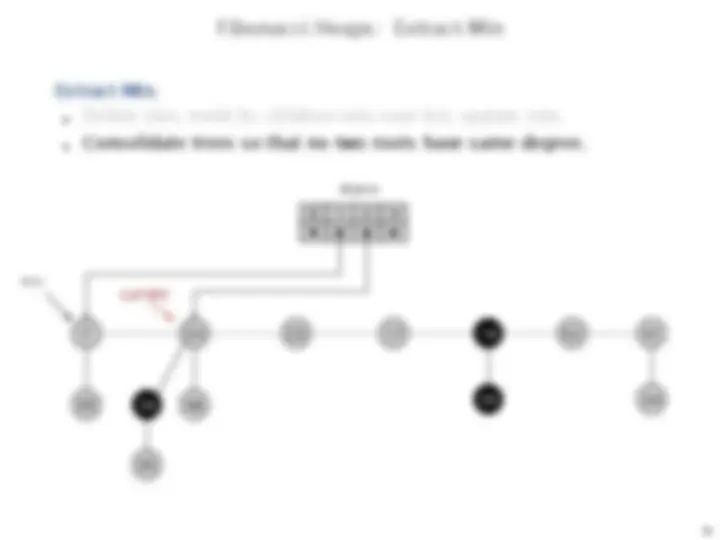
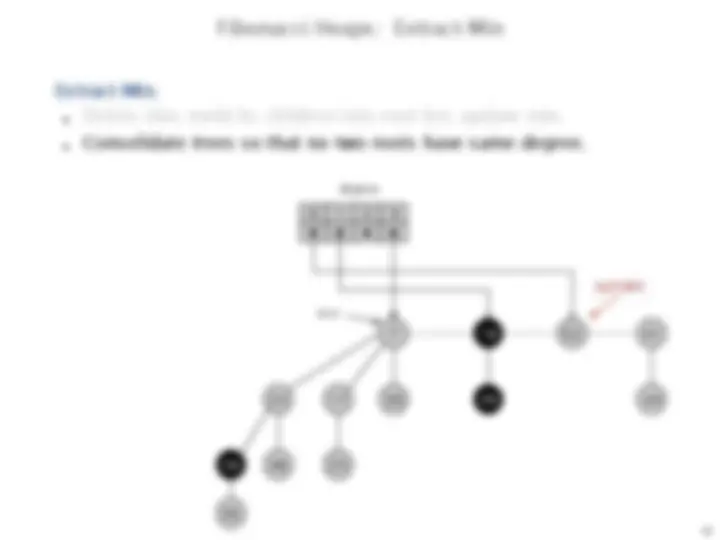
Extract-min.
Delete min; meld its children into root list; update min.
Consolidate trees so that no two roots have same degree.
min
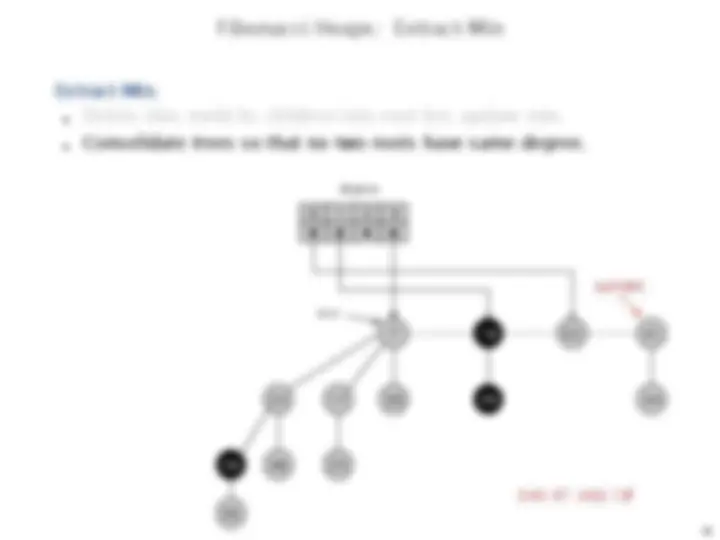
Fibonacci Heaps: Extract-Min
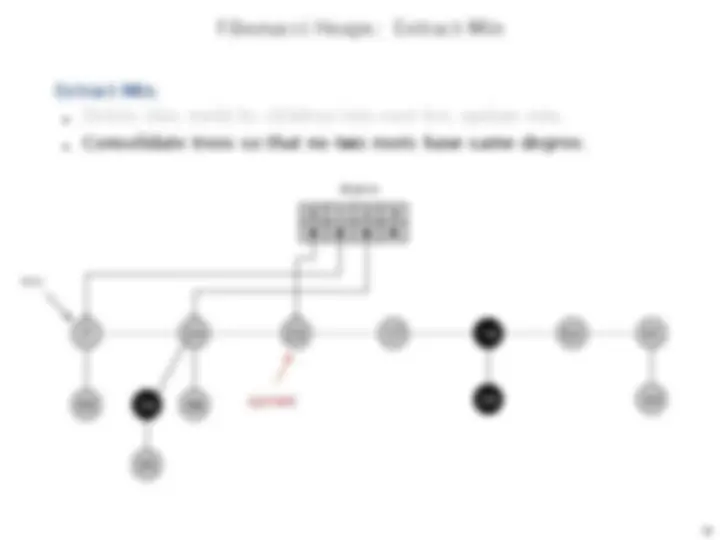
Extract-Min.
Delete min; meld its children into root list; update min.
Consolidate trees so that no two roots have same degree.
min
current
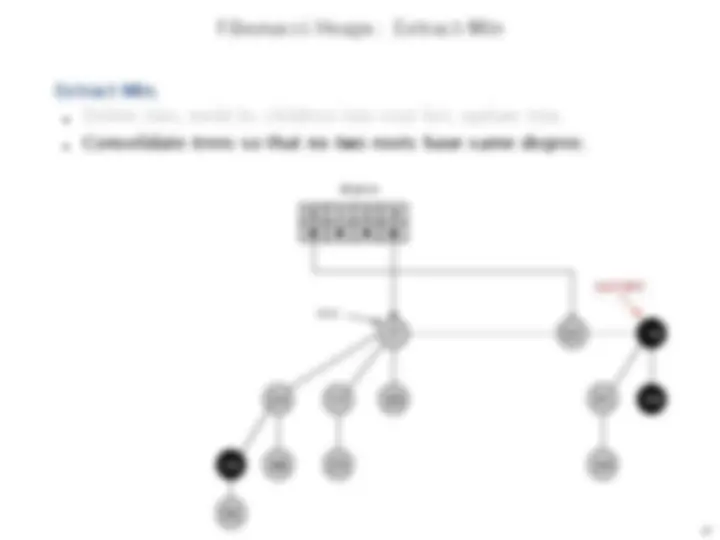
Fibonacci Heaps: Extract-Min
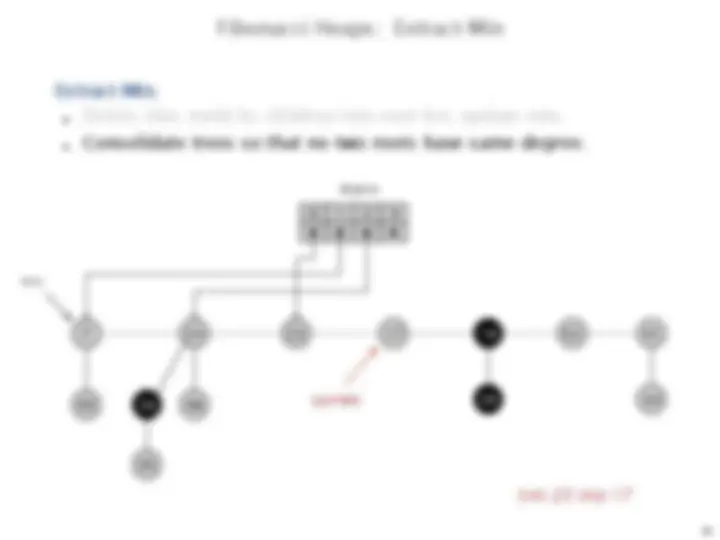
Extract-Min.
Delete min; meld its children into root list; update min.
Consolidate trees so that no two roots have same degree.
current
min
degree
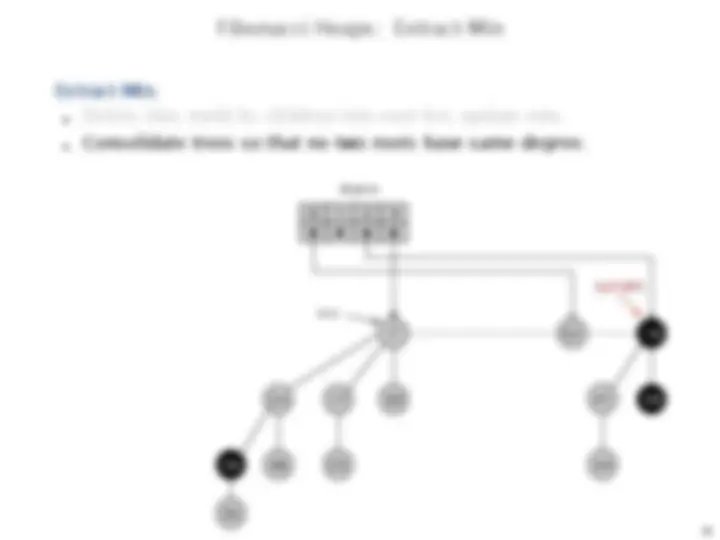
Fibonacci Heaps: Extract-Min
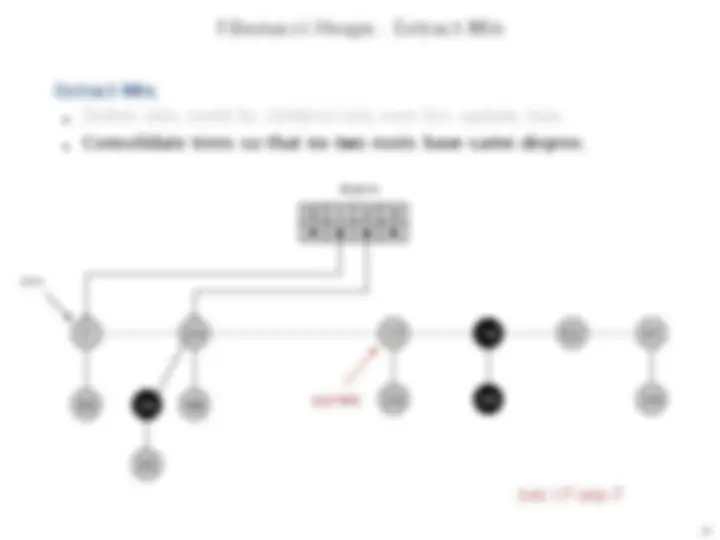
Extract-Min.
Delete min; meld its children into root list; update min.
Consolidate trees so that no two roots have same degree.
min
current
degree
Fibonacci Heaps: Extract-Min
Extract-Min.
Delete min; meld its children into root list; update min.
Consolidate trees so that no two roots have same degree.
min
current
degree
link 23 into 17