Download Control Engineering Examination for Electrical and Electronic Engineering Degree and more Exams Electrical Engineering in PDF only on Docsity!
S450 02/09/
THE MANCHESTER METROPOLITAN UNIVERSITY
FACULTY OF SCIENCE AND ENGINEERING
DEPARTMENT OF ENGINEERING AND TECHNOLOGY
SESSION 1999/
Examination for the BEng (HONS) ELECTRICAL AND ELECTRONIC ENGINEERING – FULL TIME BEng (HONS) ELECTRONIC ENGINEERING – PART TIME YEAR FOUR/FIVE
UNIT 64EE3013 : CONTROL ENGINEERING
Friday 26 May 2000
2.00 pm to 5.00 pm
Instructions to Candidates
Answer FIVE questions with not more than three from either section.
Figure Q1, Figure Q2 and Jury Contours are provided on separate sheets.
Breakdown of marks for each question are shown in square parentheses.
continued
Section A
- A precision machine tool and its associated controller is described by the transfer
function (^)
= ^ +
s ss
s a G s K where K and a are controller parameters
with a = 0.5. The root locus diagram is shown in Figure Q1.
(a) What is the system type and what is the steady state error to reference ramp inputs on closed-loop? [4 Marks]
(b) Find the gain K required to reduce steady state errors to a reference parabolic input r ( t )= 21 t^2 to less than 1%. [4 Marks]
(c) Use the root locus diagram to assess the gain K required to give the closed- loop poles a damping ratio ζ = 0.5. With this gain can the system be regarded as dominantly second order? A separate sheet with Figure Q1 is provided for your use and this should be handed in with your Answer Booklet. [8 Marks]
(d) By reference to your answers in (b) and (c) above, discuss whether it is possible to select K and a to satisfy the design criteria for both ζ and the steady state requirements simultaneously. [4 Marks]
- (a) Describe how a lag compensator may be used to improve steady state system perform ance w h ilst m aintaining relative stab ility m argins. [4 Mark s]
(b) (i) The open-loop frequency response for a process
ss s
G s is shown in Figure Q2.
Design a lag compensator s T
sT Gc s
( ) that will give steady state
errors due to ramp inputs of less than 5% and achieve a gain cross-over frequency (ωcg) of 1 rad s-1. [12 Marks]
(ii) Estimate the resulting phase margin and discuss whether additional phase lead compensation might be required. [4 Marks]
A separate sheet with Figure Q2 is provided for your use and this should be handed in with your Answer Booklet.
- The continuous time transfer function of a simple PID controller may be written as
continued
- (a) Figure Q4 shows the suspension system for a railway carriage.
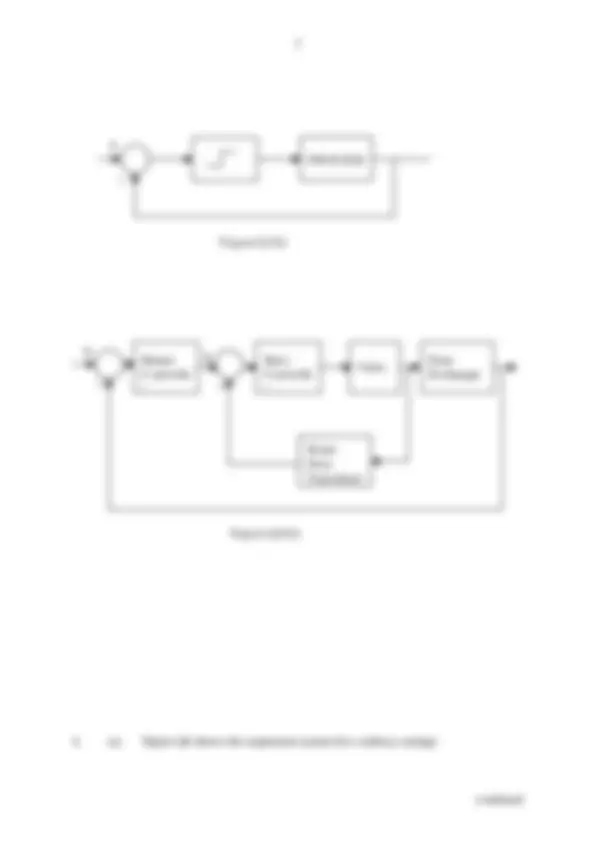
Figure Q 3(i)
Master Controlle r
Slave Controlle r
Valve H eat Exch anger
Steam Flow Transducer
Figure Q 3(ii)
PR O CESS
Question 4 continued overleaf
U(t) is the input and represents the displacement of the wheels caused by track irregularities; X 1 (t) represents the displacement of the Bogey of mass M 1 ; X 2 (t) represents the displacement of the carriage of mass M 2. Develop the system differential equations and show that the state variable model is given by:
M U
K
X
X
X
X
M
B
M
K
M
B
M
K
M
B
M
K
M
B
M
K K
X
X
X
X
1
1
2
2
1
1
2 2
2 2 2
2
1 1
2 1 1
1 2
2
2
1
1
[10 Marks]
(b) A state variable model is given by:
() [ 1 1 ] ()
X t
X(t) X(t)
y t
ut
(i) Draw an analogue simulation of this model. [5 Marks]
(ii) Derive the equivalent discrete time state model which uses a sample time T = 0.2, stating clearly the approximations you use. [5 Marks]
02/09/02 continued
SECTIO N B
- (a) Explain h ow sam pling intervalis to b e ch osen for im plem enting a digital controller in th e follow ing cases.
(i) A PID controller designed using continuous-time methods for a system with a bandwidth of 20 rad/s is to be emulated on a digital computer. [ Marks]
(ii) A minimum variance controller for a process with a dominant time- constant of 4 s is to be implemented in a direct digital control loop. [3 Marks]
(b) An open-loop system is described by the second-order difference equation yk = yk − 1 − 0. 25 yk − 2 + 0. 25 uk − 1
(i) Assuming zero initial conditions, calculate the response of the system over the first five sampling periods if a unit step input is applied to the system at time t = 0 s. [4 Marks]
(ii) Assuming z-1^ as the unit delay operator, determine the transfer function of the system and hence examine the system stability using pole-zero analysis in the z-plane. [5 Marks]
(iii) Mark the poles on the Jury contours and comment on the damping present in the system. Is the sampling rate chosen adequate for implementing a digital controller? [5 Marks]
02/09/02 continued
- (a) The bilinear transformation is commonly used to emulate continuous-time controllers on digital computers. Discuss one major problem commonly encountered in such emulation and suggest how it can be overcome. [5 Marks] (b) A lead compensator designed for a process using continuous-time method is given by the transfer function
s
s s c
G
This controller is to be implemented using a digital computer with a sampling interval of 0.1 s.
D e rive th e equivalent discrete-tim e transfer function of th e controller using th e b ilinear transform ation. D e rive a difference equation for th e control output at th e k th^ sam pling instant. [10 Mark s]
(c) Explain the implications of the non-uniqueness of the mapping of s-plane to z- plane using the equivalence z = esT. Name one significant phenomenon this gives rise to, and briefly state how this effect can be eliminated. [5 Marks]
02/09/02 continued
- (a) Th e open-loop response of a th erm alprocess to a unit step input is sh ow n in Figure 8. Determine an approximate first-order transfer function of the form
−
s
Ke Gs
TD s
τ
to represent the process.
[5 Marks]
(b) In a system identification experiment, five values of the input-output data obtained from a process are shown in Table 8. The process is to be modelled by a difference equation of the form
y (^) k + = ayk + bu k
∧ 1
where (^) + 1
∧ y (^) k represents the model output at sampling instant k+1, y (^) k , uk represent the actual process output and input at sampling instant k respectively. Using the first three input/output data points only, write down the system equations in the matrix form given by
y =Φ β where y is the output vector, Φ is the data matrix and β is the parameter vector. Using the values given show that the parameters can be estimated as a = -0. and b = 1. [9 Marks]
(c) Determine the transfer function of a dead-beat controller if a process with a first-order transfer function, G 1 (z), given below is to be driven to its set-point in one sampling instant. Briefly outline at least two problems with such control action.
z
z G z
[6 Marks]
k 1 2 3 4 5 u(k) 1.0000 -1.0000 -1.0000 1.0000 -1. y(k) -0.6914 1.3457 -1.6729 -0.1636 1.
Table 8
S450 02/09/
0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 42 44 46 48 50 52 54 56 58 60
0
1
2
3
4
5
6
7
8
9
Time s
Out
put
END
Figure 8
