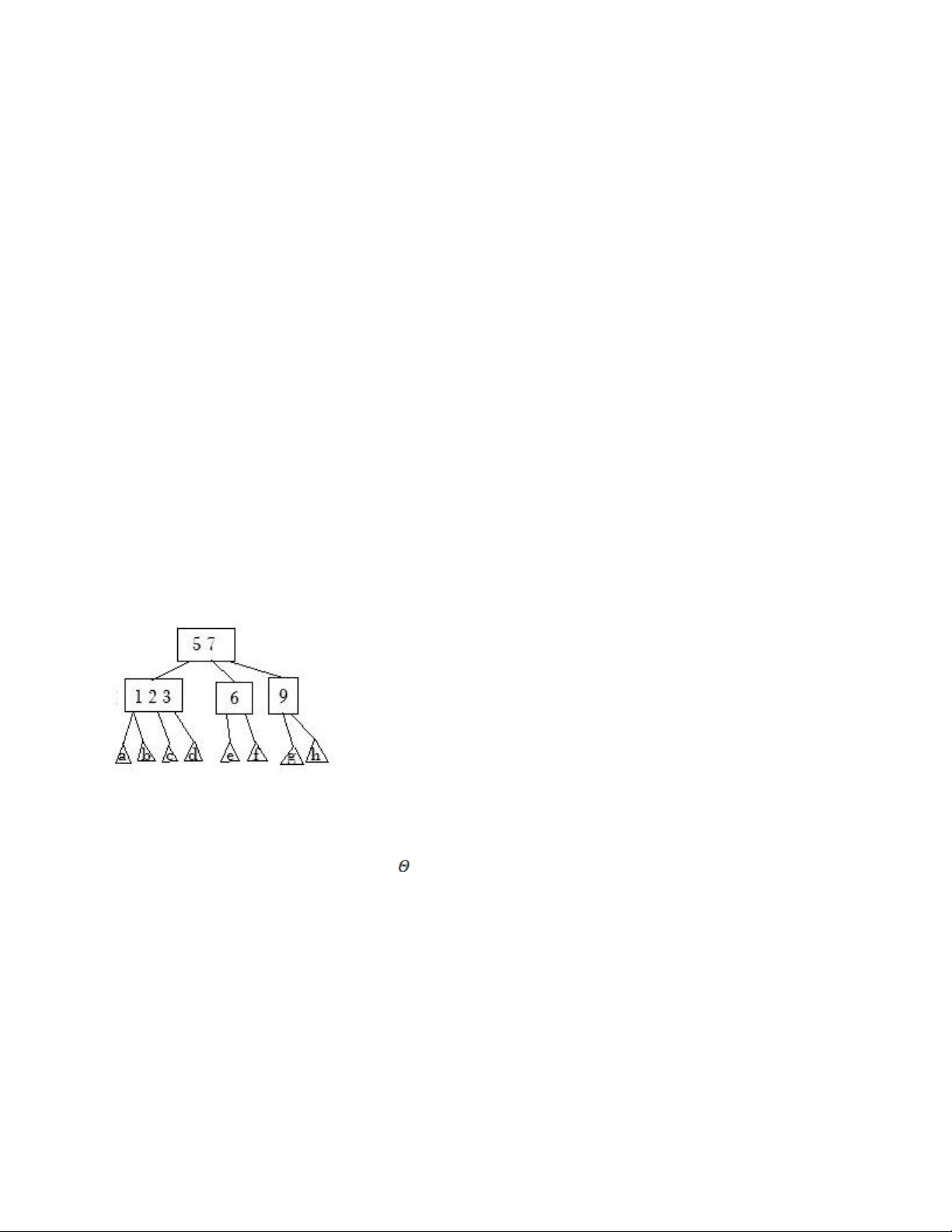
CS61B: Fall 2006, Midterm Exam II, Jo na th an Shewchuk
Problem 1. (7 p oints) A Miscella ny
a.(1 poin t) Suppose you impl ement a binar y search met hod and i t t akes 10 microseco nds t o s earch a
1,0 00 ,0 00-in t arra y for a number t ha t tur ns out no t to be in the array . How long do y ou estimat e i t
would take fo r your implemen ta ti on t o search a 1,000,00 0,000, 00 0-int array fo r a number t ha t’s n ot
in the ar ray?
b. (2 poin ts) Ex plai n why (1/(n-10 0))Є O(n). Do n’t just reiterate t he definit ion of big-Oh; give
specific values of c a nd N th at support t he clai m. (No need fo r a co mplet e proo f, th ough.)
c. (2 points) Wh en we remove a n i tem f ro m a 2 -3-4 tr ee, sometimes a node tries to “st eal” a key
fro m a sibling by p erforming a r ota tion. However, t h e remove algorithm we lear ned in class onl y
allows a node t o steal f ro m a n adjacen t sibling. But t here’s no fundamen tal reas on why a n ode
couldn’ t s teal a key from a no nadjacent sibling, excep t that we wanted to keep t he algorithm as
simple as possible.
Show how we could modify the 2- 3-4 tree below so t ha t t he “ 9” n ode has o ne mo re key, the “1 2 3”
node has one fewer key, every oth er node has t he same number o f k eys it had before, a nd the tree is
still a valid 2-3-4 tree con taining t he same ke ys it had before. Th e tri angles at the bot tom are
subtrees, which you canno t restruc ture (but you can change th eir pa ren ts).
d. (2 poin ts) Fill in t he blank. The worst -case running time o f th e following me th od, ex pressed as a
function of the input parameter n, is in (___________________________________________).
Not e th at th e loop do es not use “i - - “!
public sta tic void weirdo(lo ng n) {
Tree234 tr ee = new Tree234() ; //Construct an empty 2-3-4 tree.
for (long i = n; i > 1; i = i / 2) {
tree.inser t(i);
}
}
It’s not quite like the running time of any other algorith m you’ve seen . An explanation of your reasoning
might help you get part marks if your ans wer is wrong.)
Problem 2. (7 points) Binary Trees.
