












Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
In the subject of the Data Structures, the key concept and the main points, which are very important in the context of the data structures are listed below:Binary Search Trees, Tree Data Structure, Non-Linear Data Structure, Shape of a Tree, Children, Organizational Structure, Efficiently, Searched According, Traversed, Pictures
Typology: Slides
1 / 20

This page cannot be seen from the preview
Don't miss anything!













7/8/
1
7/8/
2
A non-linear data structure that follows theshape of a tree (i.e. root, children, branches,leaves etc)
-^
Most applications require dealing withhierarchical data (eg: organizational structure)
-^
Trees allows us to find things efficiently^ – Navigation is O(log n) for a “balanced” tree with n
nodes
A Binary Search Tree (BST) is a data structurethat can be traversed / searched according to anorder
-^
A binary tree is a tree such that each node canhave at most 2 children.
7/8/
4
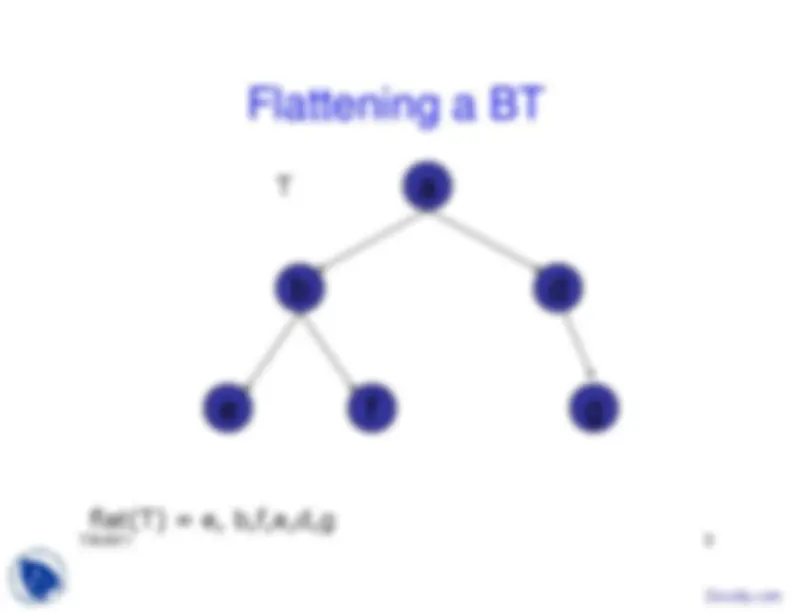
Definition of Flat T
-^
Left Tree, Then Root, then Right Tree
root
L
R
7/8/
5
T
flat(T) = e, b,f,a,d,g
7/8/
7
7/8/
8
Definitions
1
k^
k^
i+
-^
7/8/
10
Binary Tree Questions
What is the
maximum height
of a binary tree
with n nodes? What is the
minimum height
What is the minimum and maximum
number of
nodes
in a binary tree of height h?
What is the
minimum number
of nodes in a full
tree of height h?
-^
Is a complete tree a full tree?
-^
Is perfect tree a full and complete tree?
7/8/
11
Binary Tree Properties
-^
Counting Nodes in a Binary Tree^ – The max number of nodes at level
i^
is 2
i^ (i=0,1,…,h)
Find a relation between
n
and
h.
-^
A
complete tree
of height,
h
, has between 2
h^
and 2
h +
nodes.
-^
A
perfect
tree of height h has 2
h +
-1 nodes
7/8/
13
7/8/
14
Tree Operations
Tree Traversals^ –
Inorder, PreOrder, PostOrder
Level Order
Insert Node, Delete Node, Find Node
-^
Order Statistics for BST’s^ –
Find k
th^
largest element
num nodes between two values
Other operations^ – Count nodes, height of a node, height of a tree,
balanced info
7/8/
16
Inorder Traversal
private void inorder(BinaryNode root){
if (root != null) {
inorder(root.left); process root; inorder(root.right); }
}
7/8/
17
Preorder Traversal
private void preorder(BinaryNode root){
if (root != null) {
process root; preorder(root.left);preorder(root.right); }
}
7/8/
19
Level order or Breadth-first traversal •Visit nodes by levels• Root is at level zero• At each level visit nodesfrom left to right• Called “
Breadth-First-
Traversal(BFS)”
7/8/
20
Level order or Breadth-first traversal
enqueue the rootwhile (the queue is not empty){
dequeue the front elementprint itenqueue its left child (if present)enqueue its right child (if present)
BFS Algorithm