Algorithm Design Methods - Algorithms and Applications in Java - Lecture Slides, Slides of Computer Science

Download Algorithm Design Methods - Algorithms and Applications in Java - Lecture Slides and more Slides Computer Science in PDF only on Docsity!

Algorithm Design Methods

• Greedy method.
• Divide and conquer.
• Dynamic Programming.
• Backtracking.
• Branch and bound.

Some Methods Not Covered

• Linear Programming.
• Integer Programming.
• Simulated Annealing.
• Neural Networks.
• Genetic Algorithms.
• Tabu Search.

Machine Scheduling

Find a schedule that minimizes the finish time.

• optimization function … finish time
• constraints  each job is scheduled continuously on a single machine for an amount of time equal to its processing requirement  no machine processes more than one job at a time

Bin Packing

Pack items into bins using the fewest number of bins.

• optimization function … number of bins
• constraints  each item is packed into a single bin  the capacity of no bin is exceeded

Feasible And Optimal Solutions

A feasible solution is a solution that satisfies the constraints.

An optimal solution is a feasible solution that optimizes the objective/optimization function.

Greedy Method

• Solve problem by making a sequence of decisions.
• Decisions are made one by one in some order.
• Each decision is made using a greedy criterion.
• A decision, once made, is (usually) not changed later.

LPT Schedule

• LPT rule does not guarantee minimum finish time schedules.
• (LPT Finish Time)/(Minimum Finish Time) <= 4/3 - 1/(3m) where m is number of machines
• Minimum finish time scheduling is NP-hard.
• In this case, the greedy method does not work.
• The greedy method does, however, give us a good heuristic for machine scheduling.

Container Loading

• Ship has capacity c.
• m containers are available for loading.
• Weight of container i is wi.
• Each weight is a positive number.
• Sum of container weights > c.
• Load as many containers as is possible without sinking the ship. Docsity.com

Container Loading With 2 Ships

Can all containers be loaded into 2 ships whose capacity is c (each)?

• Same as bin packing with 2 bins.  Are 2 bins sufficient for all items?
• Same as machine scheduling with 2 machines.  Can all jobs be completed by 2 machines in c time units?
• NP-hard.

0/1 Knapsack Problem

0/1 Knapsack Problem

• Hiker assigns a profit/value pi to item i.
• All weights and profits are positive numbers.
• Hiker wants to select a subset of the n items to take.  The weight of the subset should not exceed the capacity of the knapsack. (constraint)  Cannot select a fraction of an item. (constraint)  The profit/value of the subset is the sum of the profits of the selected items. (optimization function)  The profit/value of the selected subset should be maximum. (optimization criterion)

0/1 Knapsack Problem

Let xi = 1 when item i is selected and let xi = 0 when item i is not selected.

i = 1

n maximize pi^ xi

i = 1

n subject to wi^ xi^ <= c

and xi = 0 or 1 for all i

Greedy Attempt 2

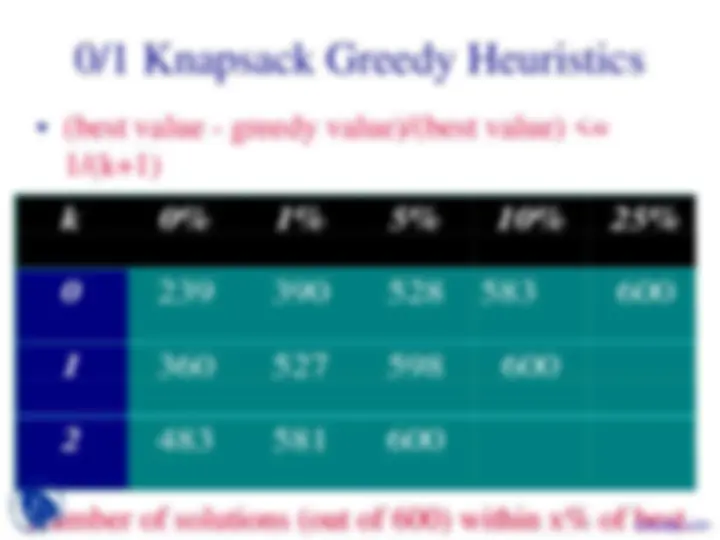
Be greedy on profit earned.

 Select items in decreasing order of profit.

n = 3, c = 7

w = [7, 3, 2]

p = [10, 8, 6]

only item 1 is selected

profit (value) of selection is 10

not best selection!

Greedy Attempt 3

Be greedy on profit density (p/w).

 Select items in decreasing order of profit density.

n = 2, c = 7

w = [1, 7]

p = [10, 20]

only item 1 is selected

profit (value) of selection is 10

not best selection!